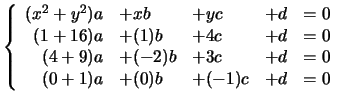Solution to Problem 2

General form of an equation of a circle can be written as

ax² + by²+ cx + dy + e =0.

STEP ONE : Substitute the general point (x,y) and the three given points in the equation to form the following homogenous linear system

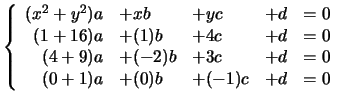$\left\{ \begin{array}{rllll} (x^2 + y^2) a &+ xb &+ yc &+ d &=0 \\ (1 +16)a &... ...-2)b &+ 3c &+ d &=0\\ (0+1)a &+ (0)b &+ (-1)c &+ d &=0\\ \end{array}\right.$ The linear system in the matrix form can be written as AX = 0 with the coeeficient matrix A

$A = \left[ \begin{array}{rrrr} x^2 + y^2 & x & y & 1 \\ 17 & 1 & 4 & 1 \\ 13 & -2 & 3 & 1 \\ 1 & 0 & -1 & 1 \end{array}\right]$ , $X= \left[ \begin{array}{r} a \\ b \\ c \\ d \end{array}\right]$ and $\left[ \begin{array}{r} 0 \\ 0 \\ 0 \\ 0 \end{array}\right]$

This linear system has a non-trivial solution if and only if $\det(A) =0.$

So, let

$\left\vert \begin{array}{rrrr} x^2 + y^2 & x & y & 1 \\ 17 & 1 & 4 & 1 \\ 13 & -2 & 3 & 1 \\ 1 & 0 & -1 & 1 \end{array}\right\vert = 0$

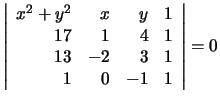
Use cofactor expansion along the first row, to obtain

$(x^2 + y^2) \left\vert \begin{array}{rrr} 1 & 4 & 1\\ -2 & 3 & 1\\ 0 & -1 & 1 \end{array}\right\vert$ $- x \left\vert \begin{array}{rrr} 17 & 4 & 1 \\ 13 & 3 & 1 \\ 1 & -1 & ... ...y}{rrr} 17 & 1 & 4\\ 13 & -2 & 3\\ 1 & 0 & -1 \end{array}\right\vert = 0$

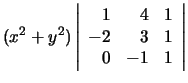
Simplify to get the equation of the circle

$$\large 14(x^2+y^2) -4x -44y -58$$

The above method described in problem 1 and 2 cam be used to fine equation of a conic section (a parabola, hyperbola or ellipse), the general from of these section is given by $\large ax^2 + by^2 + cx + dy + e =0$