SOLUTION 3: Draw a right triangle with leg one $x$, leg two $y$, and hypotenuse $z$, and assume each edge of the right triangle is a function of time $t$.
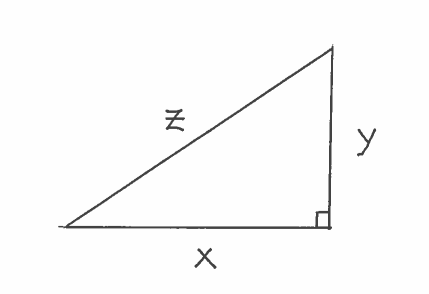
$ \ \ \ \ $ a.) Using the Pythagorean Theorem, we get the hypotenuse equation
$$ z^2=x^2+y^2 $$
GIVEN: $ \ \ \ \displaystyle{ dx \over dt } = -5 \ in/sec. \ $ and $ \ \displaystyle{ dy \over dt } = 7 \ in/sec. $
FIND: $ \ \ \ \displaystyle{ dz \over dt } $ when $ x=8 \ in. $ and $ y=6 \ in. $
Now differentiate the hypotenuse equation with respect to time $t $ getting
$$ D \{ z^2 \} = D \{x^2+y^2 \} \ \ \ \longrightarrow $$
$$ 2z \displaystyle{ dz \over dt } = 2x \displaystyle{ dx \over dt } + 2y \displaystyle{ dy \over dt } \ \ \ \longrightarrow $$
$\Big($ Multiply both sides of the equation by $1/2. \Big)$
$$ z \displaystyle{ dz \over dt } = x \displaystyle{ dx \over dt } + y \displaystyle{ dy \over dt } \ \ \ \longrightarrow $$
$\Big($ Use the Pythagorean Theorem to solve for $z$: $z^2=x^2+y^2 \ \ \rightarrow \ \ z^2=8^2+6^2=64+36=100 \ \ \rightarrow \ \ z=10.$
Now let $\displaystyle{ dx \over dt } = -5, \displaystyle{ dy \over dt } = 7, x=8, y=6, $ and $z=10. \Big) $
$$ (10) \displaystyle{ dz \over dt } = (8)(-5) + (6)(7) = 2 \ \ \ \longrightarrow $$
$$ \displaystyle{ dz \over dt } = {2 \over 10} = {1 \over 5} \ in/sec. $$
$ \ \ \ \ $ b.) The perimeter of the right triangle is
$$ P = x+y+z $$
GIVEN: $ \ \ \ \displaystyle{ dx \over dt } = -5 \ in/sec. \ $ and $ \ \displaystyle{ dy \over dt } = 7 \ in/sec. $
FIND: $ \ \ \ \displaystyle{ dP \over dt } $ when $ x=8 \ in. $ and $ y=6 \ in. $
Now differentiate the perimeter equation with respect to time $t $ getting
$$ D \{ P \} = D \{x+y+z \} \ \ \ \longrightarrow $$
$$ \displaystyle{ dP \over dt } = \displaystyle{ dx \over dt } + \displaystyle{ dy \over dt } + \displaystyle{ dz \over dt } \ \ \ \longrightarrow $$
$\Big($ Recall from solution 3 part a.): $\displaystyle{ dz \over dt } = {1 \over 5} \ in./sec$. Now let $\displaystyle{ dx \over dt } = -5, \displaystyle{ dy \over dt }=7, $ and $ \displaystyle{ dz \over dt } = {1 \over 5}. \Big) $
$$ \displaystyle{ dP \over dt } = (-5) + (8) + \Big( { 1 \over 5} \Big) \ \ \ \ \longrightarrow $$
$$ \displaystyle{ dP \over dt } = { -25 \over 5 } + { 40 \over } + (8) + { 1 \over 5} \ \ \ \ \longrightarrow $$
$$ \displaystyle{ dP \over dt } = {16 \over 5 } \ in/sec. $$
$ \ \ \ \ $ c.) The area of the right triangle is
$$ A = (1/2)(base)(height) \ \ \ \ \longrightarrow $$
$$ A = \displaystyle{1 \over 2}xy $$
GIVEN: $ \ \ \ \displaystyle{ dx \over dt } = -5 \ in/sec. \ $ and $ \ \displaystyle{ dy \over dt } = 7 \ in/sec. $
FIND: $ \ \ \ \displaystyle{ dA \over dt } $ when $ x=8 \ in. $ and $ y=6 \ in. $
Now differentiate the area equation with respect to time $t $ using the product rule getting
$$ D \{ A \} = D \{ {1 \over 2}xy \} \ \ \ \longrightarrow $$
$$ \displaystyle{ dA \over dt } = {1 \over 2} \Big( x\displaystyle{ dy \over dt } + \displaystyle{ dx \over dt } y \Big) \ \ \ \longrightarrow $$
$\Big($ Now let $\displaystyle{ dx \over dt }=-5, \displaystyle{ dy \over dt }=7, x=8, $ and $y=6. \Big) $
$$ \displaystyle{ dA \over dt } = {1 \over 2} \Big( (8)(7) + (-5) (6) \Big) = 13 \ in^2/sec. $$
Click HERE to return to the list of problems.

