Computing the Area of a Surface of Revolution

Processing math: 100%

COMPUTING THE AREA OF A SURFACE OF REVOLUTION

The following problems will use integration to find the Surface Area of a Solid of Revolution. We start with a region $R$ in the $xy$ -plane, bounded by the graphs of $y=f(x)$ , $x=a$ , $x=b$ , and the $x$ -axis. "Spin" region $R$ around the $x$ -axis to create a Solid of Revolution. Imagine the surface of this Solid of Revolution composed of consecutive thin circular ribbons. The details of this Surface Area Method are posted below.

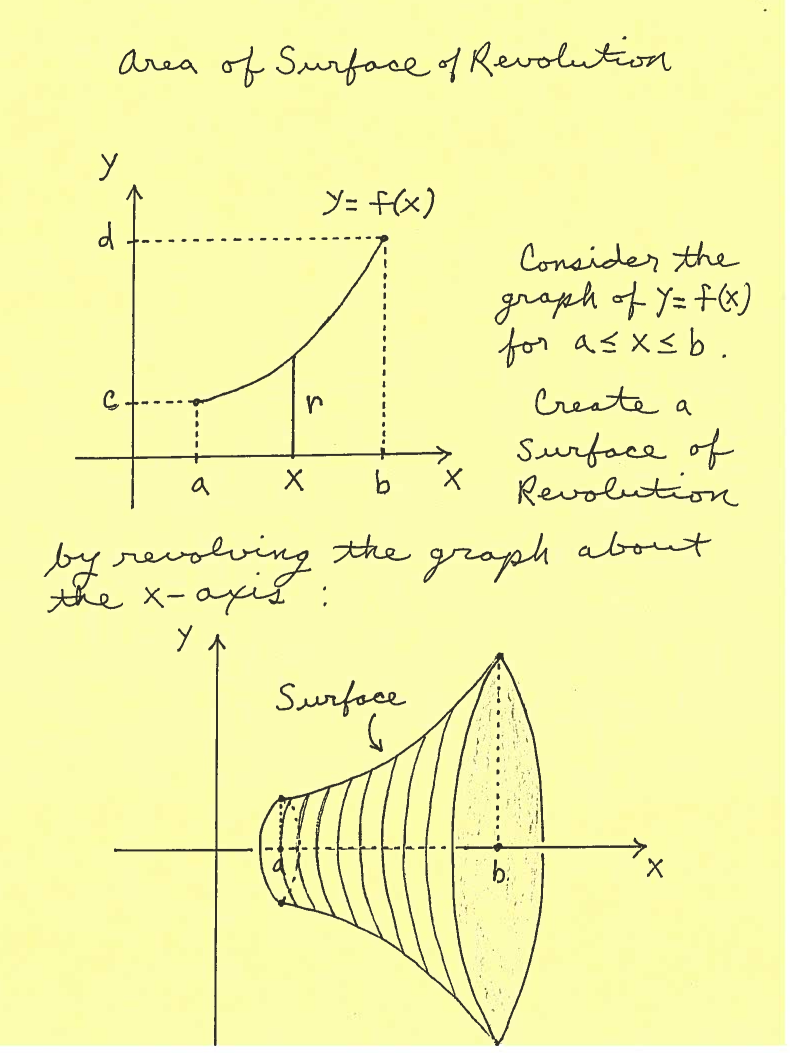
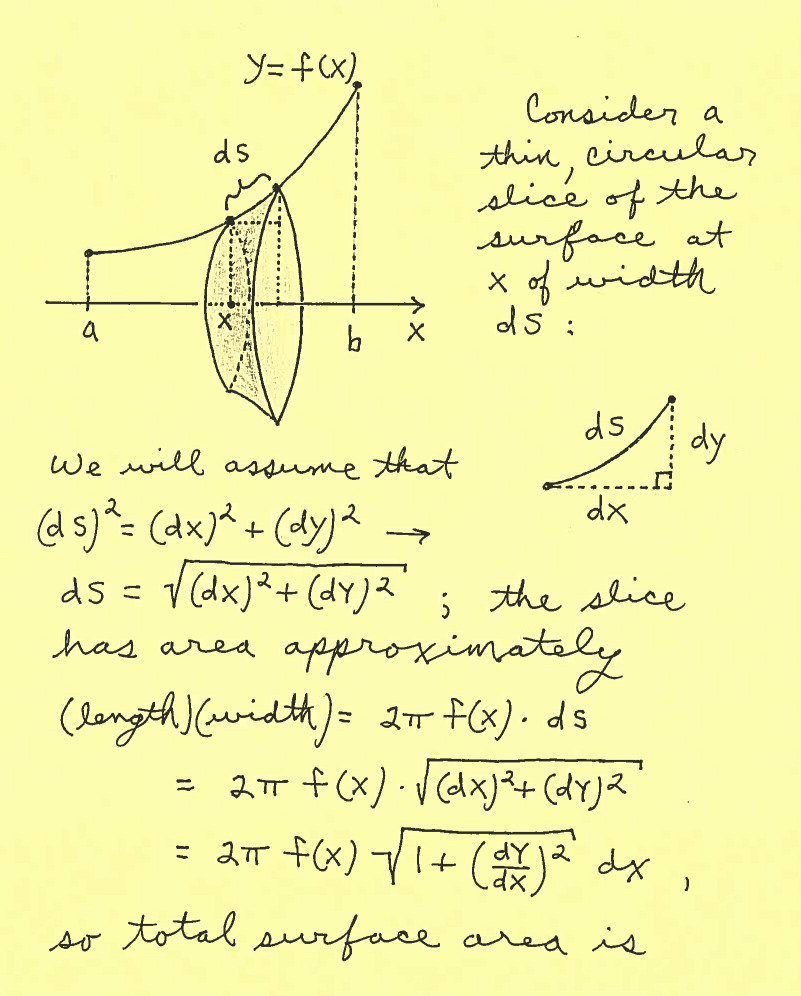
tex2html_wrap_inline125

When doing problems we will first sketch a graph of the function on a specific interval. If we are revolving the graph of

$y=f(x)$ about the

$x$ -axis, we will mark the radius

$r=f(x)$ at

$x$ on the

$x$ -axis for

$a \le x \le b$ . If we are revolving the graph of

$x=g(y)$ about the

$y$ -axis, we will mark the radius

$r=g(y)$ at

$y$ on the

$x$ -axis for

$c \le x \le d$ . Then the total Surface Area of the Surface of Revolution is either

$Surface \ Area = 2 \pi \int_{a}^{b} (radius) \sqrt{ 1 + \Big({dy \over dx}\Big)^2 } \ dx = 2 \pi \int_{a}^{b} (f(x)) \sqrt{ 1 + \Big({dy \over dx}\Big)^2 } \ dx$ or

$Surface \ Area = 2 \pi \int_{c}^{d} (radius) \sqrt{ 1 + \Big({dx \over dy}\Big)^2 } \ dy = 2 \pi \int_{c}^{d} (g(y)) \sqrt{ 1 + \Big({dx \over dy}\Big)^2 } \ dy$

EXAMPLE 1: Consider the graph of

$y=x^3$ on the interval

$0 \le x \le 2$ . Compute the Area of the Surface of Revolution formed by revolving this graph about the

$x$ -axis.

Solution: Here is a carefully labeled sketch of the graph with a radius

$r$ marked together with

$x$ on the

$x$ -axis.

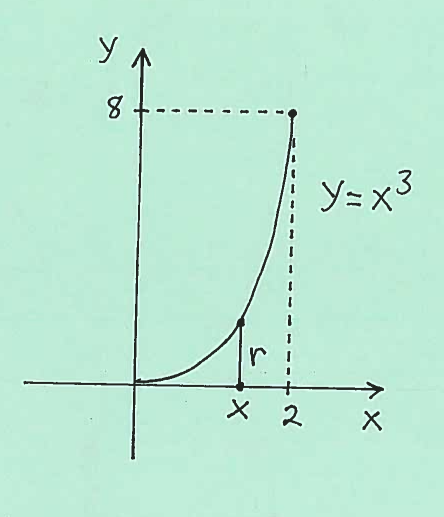
tex2html_wrap_inline125

Thus the total Area of this Surface of Revolution is

$Surface \ Area = 2 \pi \int_{0}^{2} (radius) \sqrt{ 1 + \Big({dy \over dx}\Big)^2 } \ dx$

$= 2 \pi \int_{0}^{2} (x^3) \sqrt{ 1 + (3x^2)^2 } \ dx$

$= 2 \pi \int_{0}^{2} (x^3) \sqrt{ 1 + 9x^4 } \ dx$

$= 2 \pi {2 \over 3} \cdot {1 \over 36} (1 + 9x^4)^{3/2} \Big|_{0}^{2}$

$= 2 \pi {1 \over 54} (1 + 9x^4)^{3/2} \Big|_{0}^{2}$

$= {2 \pi \over 54} (1 + 9x^4)^{3/2} \Big|_{0}^{2}$

$= { \pi \over 27 } \Big( (1 + 9(2)^4)^{3/2} - (1 + 9(0)^4)^{3/2} \Big)$

$= { \pi \over 27 } \Big( (145)^{3/2} - (1)^{3/2} \Big)$

$= { \pi \over 27 } \Big( (145)^{3/2} - 1 \Big)$

EXAMPLE 2: Consider the graph of

$y=x^2$ on the interval

$0 \le x \le 2$ . Compute the Area of the Surface of Revolution formed by revolving this graph about the

$y$ -axis.

Solution: First solve the equation for

$x$ getting

$x=y^{1/2}$ . Here is a carefully labeled sketch of the graph with a radius

$r$ marked together with

$y$ on the

$y$ -axis.

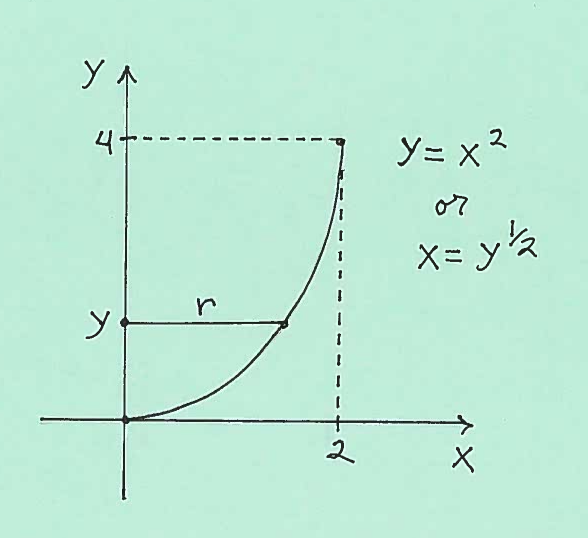
tex2html_wrap_inline125

Thus the total Area of this Surface of Revolution is

$Surface \ Area = 2 \pi \int_{0}^{4} (radius) \sqrt{ 1 + \Big({dx \over dy}\Big)^2 } \ dy$

$= 2 \pi \int_{0}^{4} (y^{1/2}) \sqrt{ 1 + ((1/2)y^{-1/2})^2 } \ dy$

$= 2 \pi \int_{0}^{4} (y^{1/2}) \sqrt{ 1 + (1/4)y^{-1} } \ dy$

$= 2 \pi \int_{0}^{4} (y^{1/2}) \sqrt{ 1 + {1 \over 4y} } \ dy$

$= 2 \pi \int_{0}^{4} (y^{1/2}) \sqrt{ {4y \over 4y}+ {1 \over 4y} } \ dy$

$= 2 \pi \int_{0}^{4} (y^{1/2}) \sqrt{ {4y +1 \over 4y} } \ dy$

$= 2 \pi \int_{0}^{4} (y^{1/2}) { \sqrt{ 4y +1 } \over \sqrt{4y} } \ dy$

$= 2 \pi \int_{0}^{4} (y^{1/2}) { \sqrt{ 4y +1 } \over 2 y^{1/2} } \ dy$

$= 2 \pi \int_{0}^{4} { \sqrt{ 4y +1 } \over 2 } \ dy$

$= {2 \pi \over 2 } \int_{0}^{4} \sqrt{ 4y +1 } \ dy$

$= \pi \cdot {2 \over 3} \cdot {1 \over 4} (4y+1)^{3/2} \Big|_{0}^{4}$

$= { \pi \over 6 } (4y+1)^{3/2} \Big|_{0}^{4}$

$= { \pi \over 6 } \Big( (4(4)+1)^{3/2} - (4(0)+1)^{3/2} \Big)$

$= { \pi \over 6 } \Big( (17)^{3/2} - (1)^{3/2} \Big)$

$= { \pi \over 6 } \Big( (17)^{3/2} - 1 \Big)$

Most of the following problems are average. A few are somewhat challenging. All are "algebra intensive" and will require that you remember your integration techniques. Many answers will have "messy numbers so be patient.

PROBLEM 1 : Consider the graphs of $y= \sqrt{x}$ on the interval $0 \le x \le 4$ . Compute the area of the surface of revolution formed by revolving this graph about the $x$ -axis.

Click HERE to see a detailed solution to problem 1.
PROBLEM 2 : Consider the graphs of $x= {1 \over 3} y^3$ on the interval $0 \le x \le 9$ . Compute the area of the surface of revolution formed by revolving this graph about the $y$ -axis.

Click HERE to see a detailed solution to problem 2.
PROBLEM 3 : Consider the graphs of $y= {4 \over 3}x^{3/4}$ on the interval $0 \le x \le 1$ . Compute the area of the surface of revolution formed by revolving this graph about the $x$ -axis.

Click HERE to see a detailed solution to problem 3.
PROBLEM 4 : Consider the graphs of $y= x^{3/2}$ on the interval $1 \le x \le 4$ . Compute the area of the surface of revolution formed by revolving this graph about the $y$ -axis.

Click HERE to see a detailed solution to problem 4.
PROBLEM 5 : Consider the graphs of $y= (2x-x^2)^{1/2}$ on the interval $0 \le x \le 2$ . Compute the area of the surface of revolution formed by revolving this graph about the $x$ -axis.

Click HERE to see a detailed solution to problem 5.
PROBLEM 6 : Consider the graphs of $y= {1 \over 6} x^3 + {1 \over 2x}$ on the interval $1 \le x \le 3$ . Compute the area of the surface of revolution formed by revolving this graph about the $x$ -axis.

Click HERE to see a detailed solution to problem 6.
PROBLEM 7 : Consider the graphs of $x = {1 \over 8} y^4 + {1 \over 4y^2}$ on the interval $1 \le y \le 2$ . Compute the area of the surface of revolution formed by revolving this graph about the $y$ -axis.

Click HERE to see a detailed solution to problem 7.
PROBLEM 8 : Consider a right circular cone of height $h$ and base radius $r$ . Find a formula for the lateral surface area (the circular base excluded) of this cone.

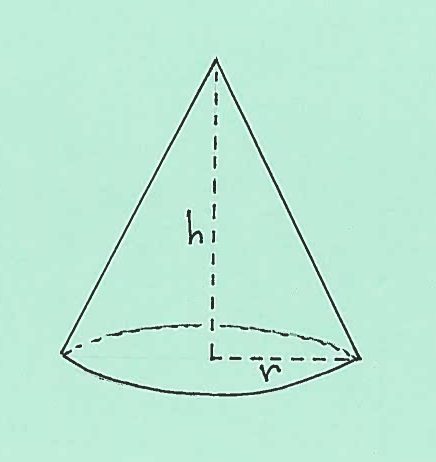
Click HERE to see a detailed solution to problem 8.
PROBLEM 9 : Consider the graph of $x^{2/3} + y^{2/3}=1$ , called an astroid. Compute the area of the surface of revolution formed by revolving this graph about the $y$ -axis.

$\ \ \$

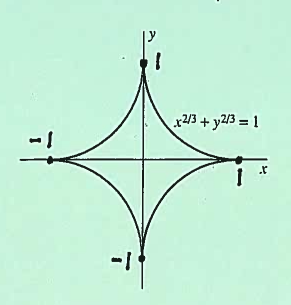Click HERE to see a detailed solution to problem 9.

Click HERE to return to the original list of various types of calculus problems.

Your comments and suggestions are welcome. Please e-mail any correspondence to Duane Kouba by clicking on the following address :

kouba@math.ucdavis.edu

A heartfelt "Thank you" goes to The MathJax Consortium and the online Desmos Grapher for making the construction of graphs and this webpage fun and easy.

Duane Kouba ... October 12, 2020