![]() ,
,
where
![]() , and
, and
![]() ,
,
where a is any positive constant not equal to 1 and ![]() is the natural (base e) logarithm of a . These formulas lead immediately to the following indefinite integrals :
is the natural (base e) logarithm of a . These formulas lead immediately to the following indefinite integrals :
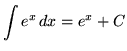
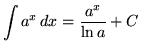
As you do the following problems, remember these three general rules for integration :
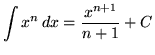 ,
,
where n is any constant not equal to -1,
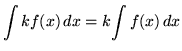 ,
,
where k is any constant, and
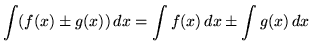 .
.
Because the integral
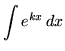 ,
,
where k is any nonzero constant, appears so often in the following set of problems, we will find a formula for it now using u-substitution so that we don't have to do this simple process each time. Begin by letting
u=kx
so that
du = k dx ,
or
(1/k)du = dx .
Now substitute into the original problem, replacing all forms of x, and getting
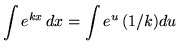
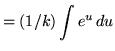
![]()
![]() .
.
We now have the following variation of formula 1.) :
3.
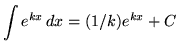 .
.
The following often-forgotten, misused, and unpopular rules for exponents will also be helpful :
![]()
and
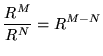 .
.
Most of the following problems are average. A few are challenging. Knowledge of the method of u-substitution will be required on many of the problems. Make precise use of the differential notation dx and du and always be careful when arithmetically and algebraically simplifying expressions.
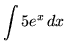 .
.
Click HERE to see a detailed solution to problem 1.
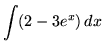 .
.
Click HERE to see a detailed solution to problem 2.
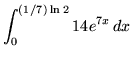 .
.
Click HERE to see a detailed solution to problem 3.
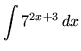 .
.
Click HERE to see a detailed solution to problem 4.
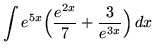 .
.
Click HERE to see a detailed solution to problem 5.
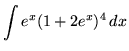 .
.
Click HERE to see a detailed solution to problem 6.
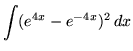 .
.
Click HERE to see a detailed solution to problem 7.
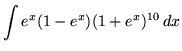 .
.
Click HERE to see a detailed solution to problem 8.
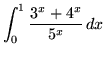 .
.
Click HERE to see a detailed solution to problem 9.
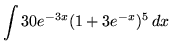 .
.
Click HERE to see a detailed solution to problem 10.
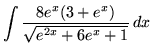 .
.
Click HERE to see a detailed solution to problem 11.
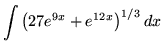 .
.
Click HERE to see a detailed solution to problem 12.
Your comments and suggestions are welcome. Please e-mail any correspondence to Duane Kouba by clicking on the following address :