Integration By Parts

THE METHOD OF INTEGRATION BY PARTS

All of the following problems use the method of integration by parts. This method uses the fact that the differential of function

For example, if

then the differential of is

Of course, we are free to use different letters for variables. For example, if

then the differential of is

When working with the method of integration by parts, the differential of a function will be given first, and the function from which it came must be determined. For example, if the differential is

$du = 2x \ dx$ ,

then the function

leads to the correct differential. In general, function

where is any real constant, leads to the correct differential

$du = 2x \ dx$ .

When using the method of integration by parts, for convenience we will always choose when determining a function (We are really finding an antiderivative when we do this.) from a given differential. For example, if the differential of is

then the constant can be "ignored" and the function (antiderivative) can be chosen to be

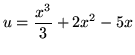$u = \displaystyle{ { x^3 \over 3 } + 2x^2 - 5x }$ .

The formula for the method of integration by parts is given by

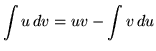$\displaystyle{ { \int u \, dv } = uv - { \int v \, du } }$ .

This formula follows easily from the ordinary product rule and the method of u-substitution. Theoretically, if an integral is too "difficult" to do, applying the method of integration by parts will transform this integral (left-hand side of equation) into the difference of the product of two functions and a new ``easier" integral (right-hand side of equation). It is assumed that you are familiar with the following rules of differentiation.

a.) $D (\sin x) = \cos x$
b.) $D (\cos x) = - \sin x$
c.) $D (\ln x) = \displaystyle{ 1 \over x }$
d.)
e.) $D (\arcsin x) = \displaystyle{ 1 \over \sqrt{ 1-x^2 } }$
f.) $D (\arctan x) = \displaystyle{ 1 \over 1 + x^2 }$

We will assume knowledge of the following well-known, basic indefinite integral formulas :

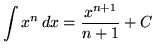$\displaystyle{ \int x^n \,dx } = \displaystyle{ {x^{n+1} \over n+1 } + C }$ , where is a constant $(n \ne -1 )$
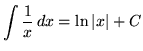
$\displaystyle{ \int { 1 \over x } \,dx } = \displaystyle{ \ln \vert x\vert + C }$
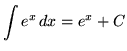
$\displaystyle{ \int e^x \,dx } = \displaystyle{ e^x + C }$
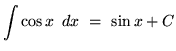
$\displaystyle{ \int \cos x \, \ dx } \ = \ \sin x + C$
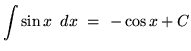
$\displaystyle{ \int \sin x \, \ dx } \ = \ - \cos x + C$
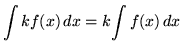$\displaystyle{ \int k f(x) \,dx } = k \displaystyle{ \int f(x) \,dx }$ , where is a constant
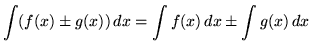
$\displaystyle{ \int ( f(x) \pm g(x) ) \,dx } = \displaystyle{ \int f(x) \,dx } \pm \displaystyle{ \int g(x) \,dx }$

Most of the following problems are average. A few are challenging. Make careful and precise use of the differential notation

and

and be careful when arithmetically and algebraically simplifying expressions.

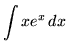PROBLEM 1 : Integrate $\displaystyle{ \int { x e^x } \,dx }$ .
Click HERE to see a detailed solution to problem 1.
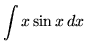PROBLEM 2 : Integrate $\displaystyle{ \int { x \sin x } \,dx }$ .
Click HERE to see a detailed solution to problem 2.
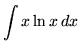PROBLEM 3 : Integrate $\displaystyle{ \int { x \ln x } \,dx }$ .
Click HERE to see a detailed solution to problem 3.
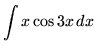PROBLEM 4 : Integrate $\displaystyle{ \int { x \cos {3x} } \,dx }$ .
Click HERE to see a detailed solution to problem 4.
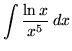PROBLEM 5 : Integrate $\displaystyle{ \int { \ln x \over x^5 } \,dx }$ .
Click HERE to see a detailed solution to problem 5.
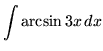PROBLEM 6 : Integrate $\displaystyle{ \int { \arcsin 3x } \,dx }$ .
Click HERE to see a detailed solution to problem 6.
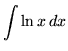PROBLEM 7 : Integrate $\displaystyle{ \int { \ln x } \,dx }$ .
Click HERE to see a detailed solution to problem 7.
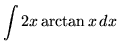PROBLEM 8 : Integrate $\displaystyle{ \int { 2x \arctan x } \,dx }$ .
Click HERE to see a detailed solution to problem 8.
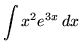PROBLEM 9 : Integrate $\displaystyle{ \int { x^2 e^{3x}} \,dx }$ .
Click HERE to see a detailed solution to problem 9.
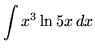PROBLEM 10 : Integrate $\displaystyle{ \int { x^3 \ln{5x} } \,dx }$ .
Click HERE to see a detailed solution to problem 10.
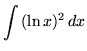PROBLEM 11 : Integrate $\displaystyle{ \int { (\ln x)^2 } \,dx }$ .
Click HERE to see a detailed solution to problem 11.
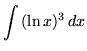PROBLEM 12 : Integrate $\displaystyle{ \int {(\ln x)^3 } \,dx }$ .
Click HERE to see a detailed solution to problem 12.
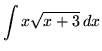PROBLEM 13 : Integrate $\displaystyle{ \int{ x\sqrt{x + 3} } \,dx }$ .
Click HERE to see a detailed solution to problem 13.
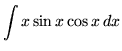PROBLEM 14 : Integrate $\displaystyle{ \int { x \sin x \cos x } \,dx }$ .
Click HERE to see a detailed solution to problem 14.
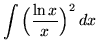PROBLEM 15 : Integrate $\displaystyle{ \int { \Big( { \ln x \over x} \Big)^2} \,dx }$ .
Click HERE to see a detailed solution to problem 15.
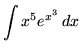PROBLEM 16 : Integrate $\displaystyle{ \int { x^5 e^{x^3} } \,dx }$ .
Click HERE to see a detailed solution to problem 16.
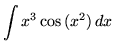PROBLEM 17 : Integrate $\displaystyle{ \int { x^3 \cos{(x^2)}} \,dx }$ .
Click HERE to see a detailed solution to problem 17.
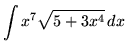PROBLEM 18 : Integrate $\displaystyle{ \int { x^7 \sqrt{5 + 3x^4} } \,dx }$ .
Click HERE to see a detailed solution to problem 18.
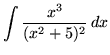PROBLEM 19 : Integrate $\displaystyle{ \int { x^3 \over (x^2 + 5)^2 } \,dx }$ .
Click HERE to see a detailed solution to problem 19.
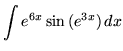PROBLEM 20 : Integrate $\displaystyle{ \int{ e^{6x} \sin{(e^{3x})} } \,dx }$ .
Click HERE to see a detailed solution to problem 20.
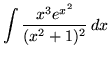PROBLEM 21 : Integrate $\displaystyle{ \int { x^3 e^{x^2} \over (x^2 + 1)^2 } \,dx }$ .
Click HERE to see a detailed solution to problem 21.
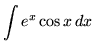PROBLEM 22 : Integrate $\displaystyle{ \int { e^x \cos x } \,dx }$ .
Click HERE to see a detailed solution to problem 22.
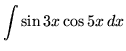PROBLEM 23 : Integrate $\displaystyle{ \int { \sin {3x} \cos{5x}} \,dx }$ .
Click HERE to see a detailed solution to problem 23.