jsMath

Introduction to Combinatorics in Sage

Trying to get oriented what is around in combinatorics ...
sage.combinat. 
       

 

Problem: A postal clerk has only 14 and 21-cent stamps. What combinations can be used to make up 3.50 Dollars worth of stamps?
sage.combinat.integer_vector_weighted?? 
       
W = WeightedIntegerVectors(350,[14,21]); W 
        
Integer vectors of 350 weighted by [14, 21]
W.cardinality() 
        
9
W.list() 
        
[[1, 16], [4, 14], [7, 12], [10, 10], [13, 8], [16, 6], [19, 4],
[22, 2], [25, 0]]

 

Let us experiment a little bit with the Fibonacci numbers. Recall that they are defined by the inital condition f_1=f_2=1 and the recursion f_{n+2} = f_{n+1} + f_n
F = [fibonacci(n) for n in range(1,15)]; F 
        
[1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144, 233, 377]
[m for m in F if is_even(m)] 
        
[2, 8, 34, 144]
sum(fibonacci(i) for i in range(1,5)) 
        
7

Defining our first function:
def sum_fib(n): return sum(fibonacci(i) for i in range(1,n+1)) 
       
[sum_fib(n) for n in range(1,13)] 
        
[1, 2, 4, 7, 12, 20, 33, 54, 88, 143, 232, 376]

Now we might conjecture that the sum of the first n Fibonacci numbers is equal to f_{n+2}-1. Let us test this conjecture!
for n in range(1,100): assert( sum_fib(n) == fibonacci(n+2)-1) print 'Done!' 
        
Done!

What would have happened if we had tried a wrong conjecture?
for n in range(1,100): assert( sum_fib(n) == fibonacci(n+2)) print 'Done!' 
        
Traceback (click to the left of this block for traceback)
...
AssertionError

 

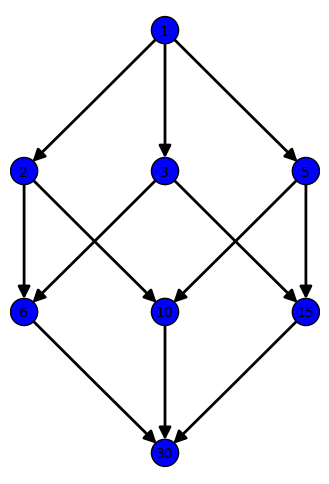
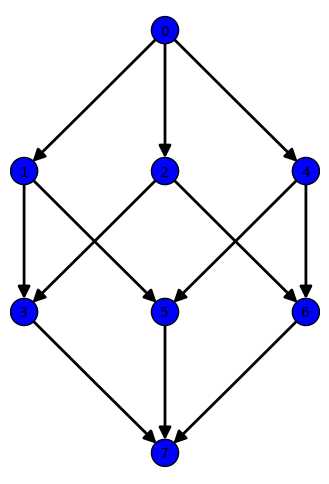
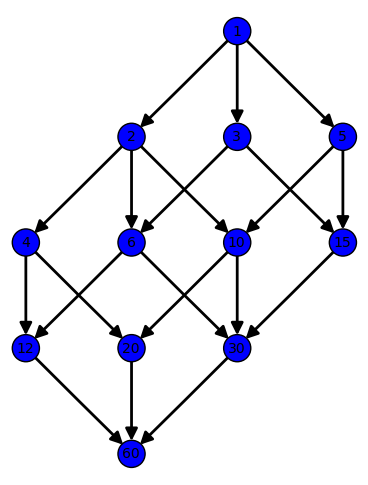
The set of all divisors of a number n form a poset by defining a<=b if a divides b.

 
n = 30 n.divisors() 
        
[1, 2, 3, 5, 6, 10, 15, 30]
def order_relation(a,b): return b%a == 0 
       
order_relation(15,30) 
        
True
order_relation(6,15) 
        
False
n = 30 P = Poset((n.divisors(), order_relation), cover_relations = False) P.plot() 
       
B = Posets.BooleanLattice(3) B.plot() 
       
n = 60 P = Poset((n.divisors(), order_relation), cover_relations = False) P.plot() 
       
P.is_graded() 
        
True
P.is_meet_semilattice() 
        
True
P.is_join_semilattice() 
        
True
P.minimal_elements() 
        
[1]
P.maximal_elements() 
        
[60]
P.mobius_function(P(1),P(30)) 
        
-1
P.mobius_function(P(1),P(4)) 
        
0
sum([P.mobius_function(P(1),v) for v in P]) 
        
0

 

Let us test some results on Mersenne numbers:
def mersenne(p): return 2^p-1 
       

Is p always prime when the Mersenne number is a prime?
[is_prime(p) for p in range(1000) if is_prime(mersenne(p))] 
        
[True, True, True, True, True, True, True, True, True, True, True,
True, True, True]

Is the converse also true?
all( is_prime(mersenne(p)) for p in range(1000) if is_prime(p) ) 
        
False

Finding the smallest counterexample:
exists( (p for p in range(1000) if is_prime(p)), lambda p: not is_prime(mersenne(p)) ) 
        
(True, 11)

 

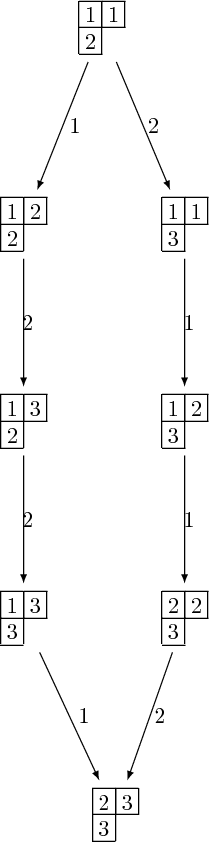
Crystal bases!!
C = CrystalOfTableaux(['A',2], shape=[2,1]) C.cardinality() 
        
8
view(C)