SOLUTION 13 : Begin with x2 + xy + y2 = 1 . Differentiate both sides of the equation, getting
D ( x2 + xy + y2 ) = D ( 1 ) ,
2x + ( xy' + (1)y ) + 2 y y' = 0 ,
so that (Now solve for y' .)
xy' + 2 y y' = - 2x - y ,
(Factor out y' .)
y' [ x + 2y ] = - 2 x - y ,
and the first derivative as a function of x and y is
(Equation 1)
![]() .
.
To find y'' , differentiate both sides of this equation, getting
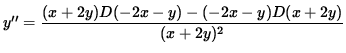
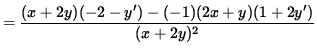
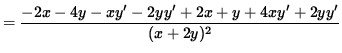
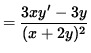 .
.
Use Equation 1 to substitute for y' , getting
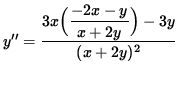
(Get a common denominator in the numerator and simplify the expression.)
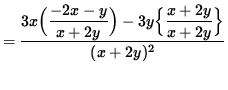
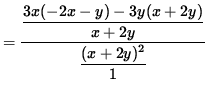
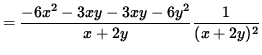
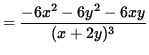 .
.
This answer can be simplified even further. Note that the original equation is
x2 + xy + y2 = 1 ,
so that
(Equation 2)
x2 + y2 = 1 - xy .
Use Equation 2 to substitute into the equation for y'' , getting
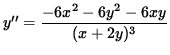
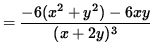
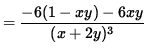
![]() ,
,
and the second derivative as a function of x and y is
![]() .
.
Click HERE to return to the list of problems.
SOLUTION 14 : Begin with x2/3 + y2/3 = 8 . Differentiate both sides of the equation, getting
D ( x2/3 + y2/3 ) = D ( 8 ) ,
D ( x2/3 ) + D ( y2/3 ) = D ( 8 ) ,
(Remember to use the chain rule on D ( y2/3 ) .)
(2/3)x-1/3 + (2/3)y-1/3 y' = 0 ,
so that (Now solve for y' .)
(2/3)y-1/3 y' = - (2/3)x-1/3 ,
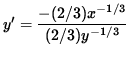 ,
,
and
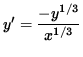 ,
,
Since lines tangent to the graph will have slope $ -1 $ , set y' = -1 , getting
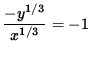 ,
,
- y1/3 = -x1/3 ,
y1/3 = x1/3 ,
( y1/3 )3 = ( x1/3 )3 ,
or
y = x .
Substitue this into the ORIGINAL equation x2/3 + y2/3 = 8 , getting
x2/3 + (x)2/3 = 8 ,
2 x2/3 = 8 ,
x2/3 = 4 ,
( x2/3 )3 = 43 ,
x2 = 64 ,
or
![]() .
.
If x=8 , then y=8 , and the tangent line passing through the point (8, 8) has slope -1 .
If x=-8 , then y=-8 , and the tangent line passing through the point (-8, -8) has slope -1 .
Click HERE to return to the list of problems.
SOLUTION 15 : Since the equation x2 - xy + y2 = 3 represents an ellipse, the largest and smallest values of y will occur at the highest and lowest points of the ellipse. This is where tangent lines to the graph are horizontal, i.e., where the first derivative y'=0 . The largest and smallest values of x will occur at the right-most and left-most points of the ellipse. This is where tangent lines to the graph are vertical, i.e., where the first derivative y' does not exist.
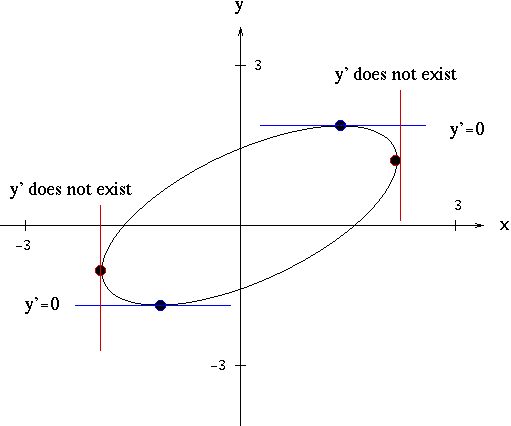
Begin by taking the derivative of both sides of the equation, getting
D ( x2 - xy + y2 ) = D ( 3 ) ,
D ( x2 ) - D ( xy ) + D ( y2 ) = D ( 3 ) ,
(Remember to use the chain rule on D ( y2 ) .)
2x - ( xy' + (1)y ) + 2 y y' = 0 ,
so that (Now solve for y' .)
2x - xy' - y + 2 y y' = 0 ,
2 y y'- xy' = y - 2x ,
(Factor out y' .)
y' [ 2y - x ] = y - 2x ,
and
(Equation 1)
![]() .
.
If the first derivative y'=0 , then (If
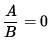 , then A=0 .)
, then A=0 .)
y - 2x = 0 ,
so that
y = 2x .
Substituting this into the original equation x2 - xy + y2 = 3 leads to
x2 - x (2x) + (2x)2 = 3 ,
x2 - 2x2 + 4x2 = 3 ,
3x2 = 3 ,
x2 = 1 ,
and
![]() .
.
Thus, the maximum value of y occurs when x=1 and y=2 , i.e., at the point
(1, 2) .
The minimum value of y occurs when x=-1 and y=-2 , i.e., at the point
(-1, -2) .
If the first derivative y' does not exist, then the denominator in Equation 1 equals zero (Why?), i.e.,
2y - x = 0 ,
so that
x = 2y .
Substituting this into the original equation x2 - xy + y2 = 3 leads to
(2y)2 - (2y) y + y2 = 3 ,
4 y2 - 2y2 + y2 = 3 ,
3y2 = 3 ,
y2 = 1 ,
and
![]() .
.
Thus, the maximum value of x occurs when y=1 and x=2 , i.e., at the point
(2, 1) .
The minimum value of x occurs when y=-1 and x=-2 , which occurs at the point
(-2, -1) .
Click HERE to return to the list of problems.
SOLUTION 16 : Begin with (x2+y2)2 = 2x2-2y2 . Differentiate both sides of the equation, getting
D (x2+y2)2 = D ( 2x2-2y2 ) ,
D (x2+y2)2 = D ( 2x2 ) - D ( 2y2 ) ,
(Remember to use the chain rule on D ( y2 ) and D ( 2y2 ) .)
2 (x2+y2) D (x2+y2) = 4x - 4 y y' ,
2 (x2+y2) (2x+2yy') = 4x - 4 y y' ,
so that (Now solve for y' .)
4x (x2+y2) + 4y(x2+y2) y' = 4x - 4 y y' ,
4 y y' + 4y(x2+y2) y' = 4x - 4x (x2+y2) ,
4 [ y y' + (x2y+y3) y'] = 4 [ x - (x3+xy2) ] ,
(Divide out 4 .)
y y' + (x2y+y3) y' = x - x3-xy2 ,
(Factor out y' .)
y' [ y + (x2y+y3) ] = x - x3-xy2 ,
and
(Equation 1)
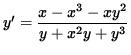 .
.
If y'=0 , then (If
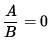 , then A=0 .)
, then A=0 .)
x - x3-xy2 = 0 ,
x (1 - x2-y2) = 0 ,
and
(**)
x = 0 or 1 - x2-y2 = 0 .
If x=0 in the original equation (x2+y2)2 = 2x2-2y2 , then
(0+y2)2 = 0-2y2 ,
y4 + 2y2 = 0 ,
y2 ( y2 + 1 ) = 0 ,
and
y=0 .
Note, however, if x=0 and y=0 are substituted into Equation 1, we get the indeterminate form " 0/0 " . Is y'=0 at the point (0, 0) , i.e., does y'(0, 0) = 0 ? We will show that the value of the derivative is NOT zero at (0, 0) . Assume that y' is continuous at (0, 0) , and that y'(0, 0) = 0 . Thus,
(Equation 2)
![]() .
.
But we also have that
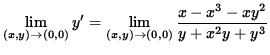
(The limit on the right-hand side takes the indeterminate form " 0/0 " , so use L'Hopital's Rule, remembering that y is an impicit function of x .)
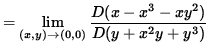
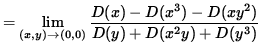
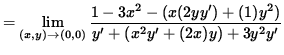
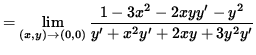
(Evaluate the limit, and use Equation 2.)
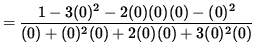
![]() .
.
Since the numerator approaches 1 and the denominator approaches 0 , this limit DOES NOT EXIST. But this contradicts Equation 2. Thus, our assumption in Equation 2 is false, and ![]() for x=0 . (NOTE: It can be shown using polar coordinates that the slope of the graph as it passes through the origin (twice !) is +1 and -1 . Returning to (**), we next have that
for x=0 . (NOTE: It can be shown using polar coordinates that the slope of the graph as it passes through the origin (twice !) is +1 and -1 . Returning to (**), we next have that
1 - x2-y2 = 0 ,
or
y2 = 1 - x2 .
Substitute this into the original equation (x2+y2)2 = 2x2-2y2 , getting
( x2+(1 - x2) )2 = 2x2-2(1 - x2) ,
1 = 2x2 - 2 + 2 x2 ,
3 = 4x2 ,
x2 = 3/4 ,
or
![]() .
.
If
![]() , then
, then
![]() . Thus y'=0 at the following points :
. Thus y'=0 at the following points :
![]() ,
,
![]() ,
,
![]() ,
,
and
![]() .
.
Click HERE to return to the list of problems.