SQUEEZE PRINCIPLE : Assume that functions f , g , and h satisfy
![]()
and
![]() .
.
Then
![]() .
.
(NOTE : The quantity A may be a finite number, ![]() , or
, or ![]() . The quantitiy L may be a finite number,
. The quantitiy L may be a finite number, ![]() , or
, or ![]() .)
.)
The Squeeze Principle is used on limit problems where the usual algebraic methods (factoring, conjugation, algebraic manipulation, etc.) are not effective. However, it requires that you be able to ``squeeze'' your problem in between two other ``simpler'' functions whose limits are easily computable and equal. The use of the Squeeze Principle requires accurate analysis, deft algebra skills, and careful use of inequalities.
Click HERE to see a detailed solution to problem 1.
Click HERE to see a detailed solution to problem 2.
Click HERE to see a detailed solution to problem 3.
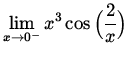 .
.
Click HERE to see a detailed solution to problem 4.
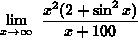 .
.
Click HERE to see a detailed solution to problem 5.
Click HERE to see a detailed solution to problem 6.
Click HERE to see a detailed solution to problem 7.
Click HERE to see a detailed solution to problem 8.
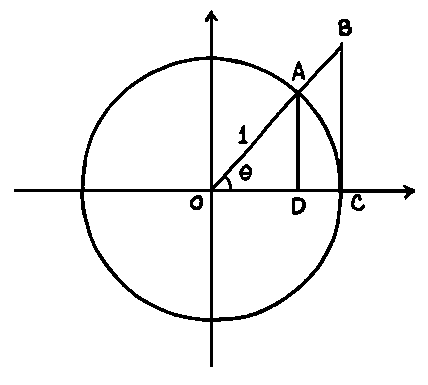
a.) By considering the areas of right triangle OAD, sector OAC, and right triangle OBC, conclude that
![]() .
.
b.) Use part a.) and the Squeeze Principle to show that
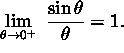
Click HERE to see a detailed solution to problem 9.
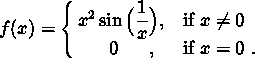
Show that f is continuous at x=0 .
Click HERE to see a detailed solution to problem 10.
Your comments and suggestions are welcome. Please e-mail any correspondence to Duane Kouba by clicking on the following address :