Next: About this document ...



SOLUTIONS TO THE LIMIT DEFINITION OF A DEFINITE INTEGRAL



SOLUTION 1 : Divide the interval $ [0, 4] $ into $ n $ equal parts each of length

$ \Delta x_{i} = \displaystyle{ 4-0 \over n } = \displaystyle{ 4 \over n } $

for $ i=1, 2, 3, ..., n $ . Choose the sampling points to be the right-hand endpoints of the subintervals and given by

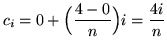
$ c_{i} = 0 + \Big( \displaystyle{ 4-0 \over n } \Big) i = \displaystyle{ 4i \over n } $

for $ i=1, 2, 3, ..., n $ . The function is

$ f(x) = 5 $ .

Then the definite integral is

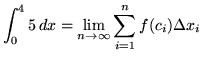
$ \displaystyle{ \int^{4}_{0} 5 \, dx} = \displaystyle{ \lim_{n \to \infty} \sum_{i=1}^{n} f(c_{i}) \Delta x_{i} } $

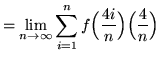
$ = \displaystyle{ \lim_{n \to \infty} \sum_{i=1}^{n} f\Big({ 4i \over n }\Big) \Big({4 \over n}\Big) } $

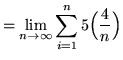
$ = \displaystyle{ \lim_{n \to \infty} \sum_{i=1}^{n} 5 \Big({4 \over n}\Big) } $

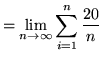
$ = \displaystyle{ \lim_{n \to \infty} \sum_{i=1}^{n} {20 \over n} } $

(Since $ i $ is the variable of the summation, the expression $ \displaystyle{20 \over n} $ is a constant. Use summation rule 1 from the beginning of this section.)

$ = \displaystyle{ \lim_{n \to \infty} n \Big( {20 \over n} \Big) } $

$ = \displaystyle{ \lim_{n \to \infty} 20 } $

$ = 20 $ .

Click HERE to return to the list of problems.




SOLUTION 2 : Divide the interval $ [0, 1] $ into $ n $ equal parts each of length

$ \Delta x_{i} = \displaystyle{ 1-0 \over n } = \displaystyle{ 1 \over n } $

for $ i=1, 2, 3, ..., n $ . Choose the sampling points to be the right-hand endpoints of the subintervals and given by

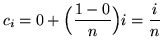
$ c_{i} = 0 + \Big( \displaystyle{ 1-0 \over n } \Big) i = \displaystyle{ i \over n } $

for $ i=1, 2, 3, ..., n $ . The function is

$ f(x) = 2x+3 $ .

Then the definite integral is

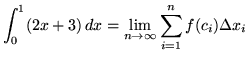
$ \displaystyle{ \int^{1}_{0} (2x+3) \, dx} = \displaystyle{ \lim_{n \to \infty} \sum_{i=1}^{n} f(c_{i}) \Delta x_{i} } $

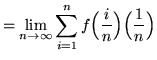
$ = \displaystyle{ \lim_{n \to \infty} \sum_{i=1}^{n} f\Big({ i \over n }\Big) \Big({1 \over n}\Big) } $

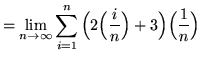
$ = \displaystyle{ \lim_{n \to \infty} \sum_{i=1}^{n} \Big(2\Big( { i \over n } \Big)+3 \Big) \Big({1 \over n}\Big) } $

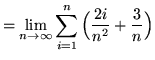
$ = \displaystyle{ \lim_{n \to \infty} \sum_{i=1}^{n} \Big( { 2i \over n^2 } + {3 \over n} \Big) } $

(Use summation rule 6 from the beginning of this section.)

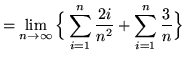
$ = \displaystyle{ \lim_{n \to \infty} \Big\{ \sum_{i=1}^{n} { 2i \over n^2 } + \sum_{i=1}^{n} {3 \over n} \Big\} } $

(Use summation rules 5 and 1 from the beginning of this section.)

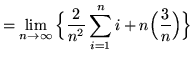
$ = \displaystyle{ \lim_{n \to \infty} \Big\{ { 2 \over n^2 }\sum_{i=1}^{n} i + n \Big({3 \over n}\Big) \Big\} } $

(Use summation rule 2 from the beginning of this section.)

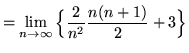
$ = \displaystyle{ \lim_{n \to \infty} \Big\{ { 2 \over n^2 } { n(n+1) \over 2 } + 3 \Big\} } $

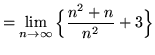
$ = \displaystyle{ \lim_{n \to \infty} \Big\{ { n^2+n \over n^2 } + 3 \Big\} } $

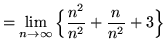
$ = \displaystyle{ \lim_{n \to \infty} \Big\{ { n^2 \over n^2 } + { n \over n^2 } + 3 \Big\} } $

$ = \displaystyle{ \lim_{n \to \infty} \Big\{ 1 + { 1 \over n } + 3 \Big\} } $

$ = \displaystyle{ \lim_{n \to \infty} \Big\{ 4 + { 1 \over n } \Big\} } $

$ = 4 + 0 $

$ = 4 $ .

Click HERE to return to the list of problems.




SOLUTION 3 : Divide the interval $ [-4, 0] $ into $ n $ equal parts each of length

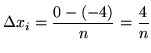
$ \Delta x_{i} = \displaystyle{ 0-(-4) \over n } = \displaystyle{ 4 \over n } $

for $ i=1, 2, 3, ..., n $ . Choose the sampling points to be the right-hand endpoints of the subintervals and given by

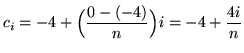
$ c_{i} = -4 + \Big( \displaystyle{ 0-(-4) \over n } \Big) i = -4 + \displaystyle{ 4i \over n } $

for $ i=1, 2, 3, ..., n $ . The function is

$ f(x) = x-2 $ .

Then the definite integral is

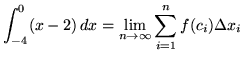
$ \displaystyle{ \int^{0}_{-4} (x-2) \, dx } = \displaystyle{ \lim_{n \to \infty} \sum_{i=1}^{n} f(c_{i}) \Delta x_{i} } $

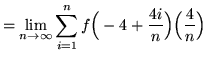
$ = \displaystyle{ \lim_{n \to \infty} \sum_{i=1}^{n} f\Big(-4+{ 4i \over n }\Big) \Big({4 \over n}\Big) } $

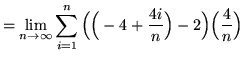
$ = \displaystyle{ \lim_{n \to \infty} \sum_{i=1}^{n} \Big( \Big(-4+{ 4i \over n } \Big) -2 \Big) \Big({4 \over n}\Big) } $

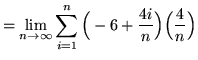
$ = \displaystyle{ \lim_{n \to \infty} \sum_{i=1}^{n} \Big( -6+{ 4i \over n } \Big) \Big({4 \over n}\Big) } $

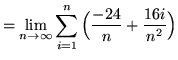
$ = \displaystyle{ \lim_{n \to \infty} \sum_{i=1}^{n} \Big( { -24 \over n } + {16i \over n^2} \Big) } $

(Use summation rule 6 from the beginning of this section.)

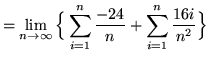
$ = \displaystyle{ \lim_{n \to \infty} \Big\{ \sum_{i=1}^{n} {-24 \over n } + \sum_{i=1}^{n} {16i \over n^2} \Big\} } $

(Use summation rules 1 and 5 from the beginning of this section.)

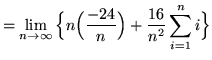
$ = \displaystyle{ \lim_{n \to \infty} \Big\{ n \Big({-24 \over n}\Big) + { 16 \over n^2 }\sum_{i=1}^{n} i \Big\} } $

(Use summation rule 2 from the beginning of this section.)

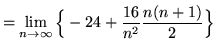
$ = \displaystyle{ \lim_{n \to \infty} \Big\{ -24 + { 16 \over n^2 } { n(n+1) \over 2 } \Big\} } $

$ = \displaystyle{ \lim_{n \to \infty} \Big\{ -24 + 8 \Big( { n+1 \over n } \Big) \Big\} } $

$ = \displaystyle{ \lim_{n \to \infty} \Big\{ -24 + 8 \Big( { n \over n } + { 1 \over n } \Big) \Big\} } $

$ = \displaystyle{ \lim_{n \to \infty} \Big\{ -24 + 8 \Big( 1 + { 1 \over n } \Big) \Big\} } $

$ = -24 + 8(1+0) $

$ = -16 $ .

Click HERE to return to the list of problems.




SOLUTION 4 : Divide the interval $ [0, 3] $ into $ n $ equal parts each of length

$ \Delta x_{i} = \displaystyle{ 3-0 \over n } = \displaystyle{ 3 \over n } $

for $ i=1, 2, 3, ..., n $ . Choose the sampling points to be the right-hand endpoints of the subintervals and given by

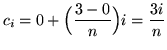
$ c_{i} = 0 + \Big( \displaystyle{ 3-0 \over n } \Big) i = \displaystyle{ 3i \over n } $

for $ i=1, 2, 3, ..., n $ . The function is

$ f(x) = x^2-1 $ .

Then the definite integral is

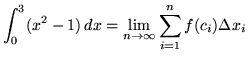
$ \displaystyle{ \int^{3}_{0} (x^2-1) \, dx } = \displaystyle{ \lim_{n \to \infty} \sum_{i=1}^{n} f(c_{i}) \Delta x_{i} } $

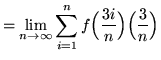
$ = \displaystyle{ \lim_{n \to \infty} \sum_{i=1}^{n} f\Big({ 3i \over n }\Big) \Big({3 \over n}\Big) } $

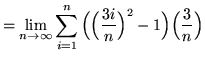
$ = \displaystyle{ \lim_{n \to \infty} \sum_{i=1}^{n} \Big( \Big({ 3i \over n } \Big)^2 - 1 \Big) \Big({3 \over n}\Big) } $

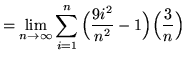
$ = \displaystyle{ \lim_{n \to \infty} \sum_{i=1}^{n} \Big( { 9i^2 \over n^2 } - 1 \Big) \Big({3 \over n}\Big) } $

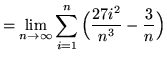
$ = \displaystyle{ \lim_{n \to \infty} \sum_{i=1}^{n} \Big( { 27i^2 \over n^3 } - {3 \over n} \Big) } $

(Use summation rule 6 from the beginning of this section.)

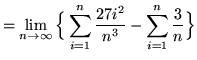
$ = \displaystyle{ \lim_{n \to \infty} \Big\{ \sum_{i=1}^{n} { 27i^2 \over n^3 } - \sum_{i=1}^{n} {3 \over n} \Big\} } $

(Use summation rules 5 and 1 from the beginning of this section.)

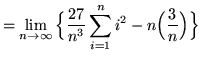
$ = \displaystyle{ \lim_{n \to \infty} \Big\{ { 27 \over n^3 }\sum_{i=1}^{n} i^2 - n \Big({3 \over n}\Big) \Big\} } $

(Use summation rule 2 from the beginning of this section.)

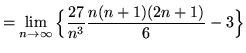
$ = \displaystyle{ \lim_{n \to \infty} \Big\{ { 27 \over n^3 } { n(n+1)(2n+1) \over 6 } - 3 \Big\} } $

$ = \displaystyle{ \lim_{n \to \infty} \Big\{ {9 \over 2} { n \over n }{ n+1 \over n }{ 2n+1 \over n } - 3 \Big\} } $

$ = \displaystyle{ \lim_{n \to \infty} \Big\{ {9 \over 2} (1)\Big({ n \over n }+{ 1 \over n }\Big) \Big({ 2n \over n }+{ 1 \over n }\Big) - 3 \Big\} } $

$ = \displaystyle{ \lim_{n \to \infty} \Big\{ {9 \over 2} \Big( 1+{ 1 \over n }\Big) \Big(2+{ 1 \over n }\Big) - 3 \Big\} } $

$ = \displaystyle{ {9 \over 2}(1+0)(2+0) - 3 } $

$ = 6 $ .

Click HERE to return to the list of problems.




SOLUTION 5 : Divide the interval $ [0, 1] $ into $ n $ equal parts each of length

$ \Delta x_{i} = \displaystyle{ 1-0 \over n } = \displaystyle{ 1 \over n } $

for $ i=1, 2, 3, ..., n $ . Choose the sampling points to be the right-hand endpoints of the subintervals and given by

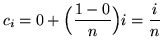
$ c_{i} = 0 + \Big( \displaystyle{ 1-0 \over n } \Big) i = \displaystyle{ i \over n } $

for $ i=1, 2, 3, ..., n $ . The function is

$ f(x) = x^2-x+3 $ .

Then the definite integral is

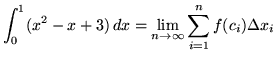
$ \displaystyle{ \int^{1}_{0} (x^2-x+3) \, dx } = \displaystyle{ \lim_{n \to \infty} \sum_{i=1}^{n} f(c_{i}) \Delta x_{i} } $

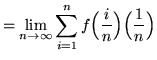
$ = \displaystyle{ \lim_{n \to \infty} \sum_{i=1}^{n} f\Big({ i \over n }\Big) \Big({1 \over n}\Big) } $

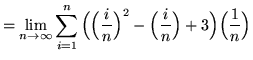
$ = \displaystyle{ \lim_{n \to \infty} \sum_{i=1}^{n} \Big( \Big({ i \over n } \Big)^2 - \Big({ i \over n } \Big) + 3 \Big) \Big({1 \over n}\Big) } $

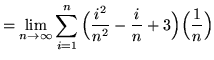
$ = \displaystyle{ \lim_{n \to \infty} \sum_{i=1}^{n} \Big( { i^2 \over n^2 } - { i \over n } + 3 \Big) \Big({1 \over n}\Big) } $

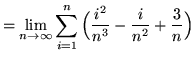
$ = \displaystyle{ \lim_{n \to \infty} \sum_{i=1}^{n} \Big( { i^2 \over n^3 } - { i \over n^2 } + { 3 \over n } \Big) } $

(Use summation rule 6 from the beginning of this section.)

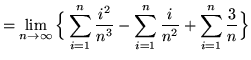
$ = \displaystyle{ \lim_{n \to \infty} \Big\{ \sum_{i=1}^{n} { i^2 \over n^3 } - \sum_{i=1}^{n} { i \over n^2 } + \sum_{i=1}^{n} {3 \over n} \Big\} } $

(Use summation rules 5 and 1 from the beginning of this section.)

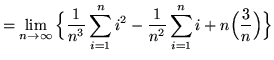
$ = \displaystyle{ \lim_{n \to \infty} \Big\{ { 1 \over n^3 }\sum_{i=1}^{n} i^2 - { 1 \over n^2 }\sum_{i=1}^{n} i + n \Big({3 \over n}\Big) \Big\} } $

(Use summation rule 2 from the beginning of this section.)

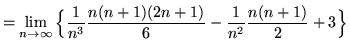
$ = \displaystyle{ \lim_{n \to \infty} \Big\{ { 1 \over n^3 } { n(n+1)(2n+1) \over 6 } - { 1 \over n^2 } { n(n+1) \over 2 } + 3 \Big\} } $

$ = \displaystyle{ \lim_{n \to \infty} \Big\{ {1 \over 6} { n \over n }{ n+1 \... ... n }{ 2n+1 \over n } - {1 \over 2} { n \over n }{ n+1 \over n } + 3 \Big\} } $

$ = \displaystyle{ \lim_{n \to \infty} \Big\{ {1 \over 6} (1)\Big({ n \over n ... ...n }\Big) - {1 \over 2} (1)\Big({ n \over n }+{ 1 \over n }\Big) + 3 \Big\} } $

$ = \displaystyle{ \lim_{n \to \infty} \Big\{ {1 \over 6} \Big( 1+{ 1 \over n ... ...g(2+{ 1 \over n }\Big) - {1 \over 2} \Big( 1+{ 1 \over n }\Big) + 3 \Big\} } $

$ = \displaystyle{ {1 \over 6}(1+0)(2+0) - {1 \over 2}(1+0) + 3 } $

$ = \displaystyle{ {1 \over 3} - {1 \over 2} + 3 } $

$ = \displaystyle{ 17 \over 6 } $ .

Click HERE to return to the list of problems.




Next: About this document ...
Duane Kouba 2000-06-08