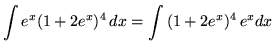
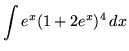 . Use u-substitution. Let
. Use u-substitution. Let
u = 1+2ex
so that
du = 2ex dx ,
or
(1/2) du = ex dx .
Substitute into the original problem, replacing all forms of x, getting
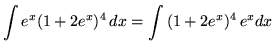
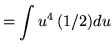
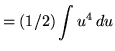
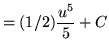
![]()
![]() .
.
Click HERE to return to the list of problems.
SOLUTION 7 : Integrate
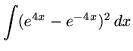 .
First, square the exponential function, recalling that
(A-B)2 = A2 - 2AB + B2 . The result is
.
First, square the exponential function, recalling that
(A-B)2 = A2 - 2AB + B2 . The result is
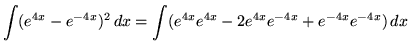
(Recall that
![]() .)
.)
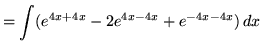
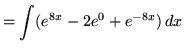
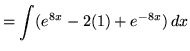
(Use the properties of integrals.)
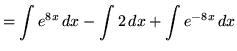
(Use formula 3 from the introduction to this section on integrating exponential functions.)
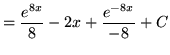
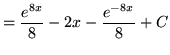 .
.
Click HERE to return to the list of problems.
SOLUTION 8 : Integrate
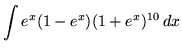 . Use u-substitution. Let
. Use u-substitution. Let
u = 1+ex
so that
du = ex dx .
In addition, we can "back substitute" with
ex = u-1 .
Substitute into the original problem, replacing all forms of x, getting
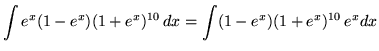
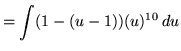
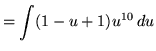
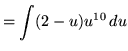
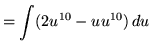
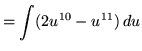
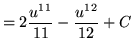
![]() .
.
Click HERE to return to the list of problems.
SOLUTION 9 :Integrate
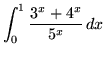 . First, split the function into two parts, getting
. First, split the function into two parts, getting
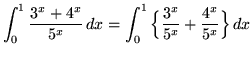
(Recall that
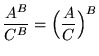 .)
.)
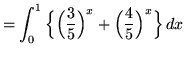
(Use formula 2 from the introduction to this section on integrating exponential functions.)
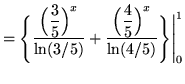
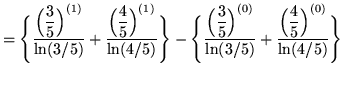
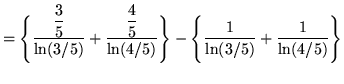
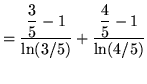
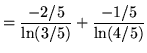 .
.
Click HERE to return to the list of problems.