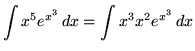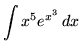Next: About this document ...



SOLUTIONS TO INTEGRATION BY PARTS



SOLUTION 16 : Integrate $ \displaystyle{ \int {x^5 e^{x^3} } \,dx } $ . Note that

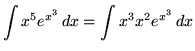$ \displaystyle{ \int {x^5 e^{x^3} } \,dx } = \displaystyle{ \int {x^3 x^2 e^{x^3} } \,dx } $ .

Now let

$ u = x^3 \ \ $ and $ \ \ dv = x^2 e^{x^3} dx $

so that

$ du = 3x^2 dx \ \ $ and $ \ \ v = \displaystyle{ (1/3) e^{x^3}} $ .

Therefore,

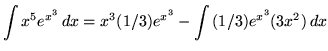
$ \displaystyle{ \int {x^5 e^{x^3} } \,dx } = \displaystyle{ x^3 (1/3) e^{x^3} - \int { (1/3) e^{x^3} } (3x^2) \, dx } $

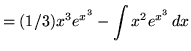
$ = \displaystyle{(1/3) x^3 e^{x^3} - \int { x^2 e^{x^3} } \, dx } $

$ = \displaystyle{ (1/3) x^3 e^{x^3} - (1/3) e^{x^3} + C } $ .

Click HERE to return to the list of problems.




SOLUTION 17 : Integrate 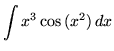$ \displaystyle{ \int {x^3 \cos{(x^2)} } \,dx } $ . Note that

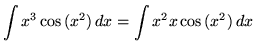$ \displaystyle{ \int {x^3 \cos{(x^2)} } \,dx} =\displaystyle{ \int {x^2 x\cos{(x^2)} } \,dx}$ .

Let

$ u = x^2 \ \ $ and $ \ \ dv = x \cos (x^2) dx $

so that

$ du = 2x \ dx \ \ $ and $ \ \ v = (1/2) \sin (x^2) $ .

Therefore,

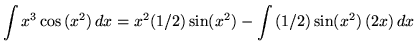
$ \displaystyle{ \int {x^3 \cos{(x^2)} } \,dx } = \displaystyle{ x^2 (1/2) \sin(x^2) - \int { (1/2) \sin (x^2) } \, (2x) \, dx } $

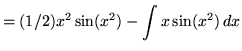
$ = \displaystyle{ (1/2) x^2 \sin (x^2) - \int { x \sin (x^2) } \, dx } $

$ = \displaystyle{ (1/2) x^2 \sin (x^2) - (1/2) ( -\cos (x^2) ) + C } $

$ = \displaystyle{ (1/2) x^2 \sin (x^2) + (1/2) \cos (x^2) + C } $ .

Click HERE to return to the list of problems.




SOLUTION 18 : Integrate 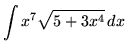$ \displaystyle{ \int {x^7 \sqrt{5 + 3x^4} } \,dx } $ . Note that

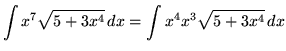$ \displaystyle{ \int {x^7 \sqrt{5 + 3x^4}} \,dx} = \displaystyle{\int {x^4 x^3 \sqrt{5 + 3x^4}} \,dx } $ .

Let

$ u = x^4 \ \ $ and $ \ \ dv = x^3 \sqrt{5 + 3x^4} \ dx = x^3 (5+3x^4)^{1/2} \ dx $

so that

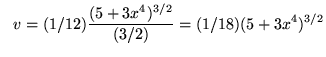$ du = 4x^3 dx \ \ $ and $ \ \ v = \displaystyle{(1/12) { (5+3x^4)^{3/2} \over (3/2) } } = (1/18) (5+3x^4)^{3/2} $ .

Therefore,

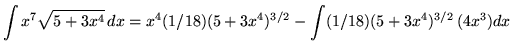
$ \displaystyle{ \int {x^7 \sqrt{5 + 3x^4} } \,dx } = \displaystyle{ x^4 (1/18)(5+3x^4)^{3/2} - \int (1/18) (5+3x^4)^{3/2} \, (4x^3) dx} $

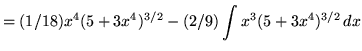
$ = \displaystyle{ (1/18)x^4 (5+3x^4)^{3/2}- (2/9)\int{ x^3(5+3x^4)^{3/2} }\, dx} $

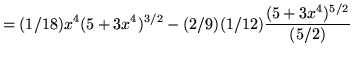$ = \displaystyle{ (1/18)x^4 (5+3x^4)^{3/2}- (2/9) (1/12){(5+3x^4)^{5/2} \over (5/2) } } $ + C

$ = (1/18)x^4 (5+3x^4)^{3/2}- (1/135)(5+3x^4)^{5/2} $ + C .

Click HERE to return to the list of problems.




SOLUTION 19 : Integrate 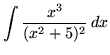$ \displaystyle{ \int { x^3 \over (x^2 + 5)^2 } \,dx } $ . Note that

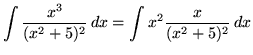$ \displaystyle{ \int { x^3 \over (x^2 + 5)^2 } \,dx } =\displaystyle{ \int { x^2 {x \over (x^2 + 5)^2} } \,dx } $ .

Let

$ u = x^2 \ \ $ and $ \ \ dv = \displaystyle{ x \over (x^2 + 5)^2 } = \displaystyle{ x (x^2 + 5)^{-2} } $

so that

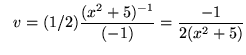$ du = 2x \ dx \ \ $ and $ \ \ v = (1/2)\displaystyle{ (x^2 + 5)^{-1} \over (-1) } = \displaystyle{ -1 \over 2(x^2 + 5) } $ .

Therefore,

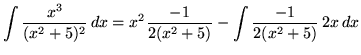
$ \displaystyle{ \int {x^3 \over (x^2 + 5)^2 } \,dx } = \displaystyle{ x^2 {-1 \over 2(x^2 + 5)} - \int { {-1 \over 2(x^2 + 5) }} \, 2x \, dx } $

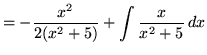
$ = \displaystyle{ -{x^2 \over 2(x^2 + 5)} + \int { {x \over x^2 + 5 }} \, dx } $

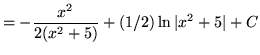$ = \displaystyle{ -{x^2 \over 2(x^2 + 5)} + (1/2) \ln \vert x^2 + 5\vert + C} $ .

Click HERE to return to the list of problems.




SOLUTION 20 : Integrate 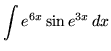$ \displaystyle{ \int { e^{6x} \sin{e^{3x}} } \,dx } $ . Note that

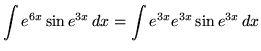$ \displaystyle{ \int { e^{6x} \sin{e^{3x}} } \,dx } = \displaystyle{ \int { e^{3x} e^{3x} \sin{e^{3x}} } \,dx } $ .

Let

$ u = e^{3x} \ \ $ and $ \ \ dv = e^{3x} \sin {e^{3x}} dx $

so that

$ du = 3 e^{3x} dx \ \ $ and $ \ \ v = (1/3)( -\cos e^{3x} ) = -(1/3) \cos e^{3x} $ .

Therefore,

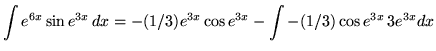
$ \displaystyle{ \int { e^{6x} \sin{e^{3x}} } \,dx } = \displaystyle{ -(1/3) e^{3x} \cos { e^{3x}} - \int { -(1/3) \cos {e^{3x} }} \,{3 e^{3x}}dx } $

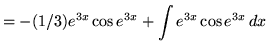
$ = \displaystyle{ -(1/3) e^{3x} \cos { e^{3x}} + \int e^{3x} \cos {e^{3x} } \,dx } $

$ = \displaystyle{ -(1/3) e^{3x} \cos { e^{3x}} + (1/3) \sin{e^{3x}} + C } $ .

Click HERE to return to the list of problems.




SOLUTION 21 : Integrate 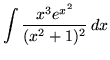$ \displaystyle{ \int {x^3 e^{x^2} \over (x^2 + 1)^2 } \,dx } $ . Note that

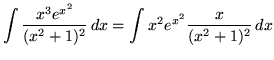$ \displaystyle{ \int {x^3 e^{x^2} \over (x^2 + 1)^2 } \,dx = \int x^2 e^{x^2} { x \over (x^2 + 1)^2 } \,dx } $ .

Let

$ u = x^2 e^{x^2} \ \ $ and $ \ \ dv = \displaystyle{x \over (x^2 + 1)^2} dx = x (x^2 + 1)^{-2} dx $

so that

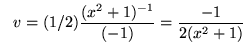$ du = \Big( 2x e^{x^2} + x^2 (2x) e^{x^2} \Big) dx = 2xe^{x^2} (1 + x^2) dx \ \ $ and $ \ \ v = \displaystyle{ (1/2){ (x^2 + 1)^{-1} \over (-1) } = { -1 \over 2(x^2 + 1) } } $ .

Therefore,

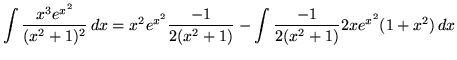
$ \displaystyle{ \int { {x^3 e^{x^2} \over (x^2 + 1)^2} } \,dx } = \displaysty... ...{-1 \over 2(x^2+1)} - \int {{-1 \over 2(x^2+1)} 2x e^{x^2} ( 1 + x^2) } \,dx } $

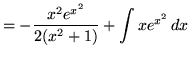
$ = \displaystyle{ -{x^2 e^{x^2} \over 2(x^2+1)} + \int { x e^{x^2} } \,dx} $

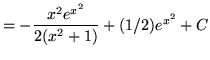$ = \displaystyle{ -{x^2 e^{x^2} \over 2(x^2+1)} + (1/2) e^{x^2} + C } $ .

Click HERE to return to the list of problems.




SOLUTION 22 : Integrate 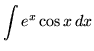$ \displaystyle{ \int {e^x\cos{x} } \,dx } $ . Let

$ u = e^x \ \ $ and $ \ \ dv = \cos x \ dx $

so that

$ du = e^x dx \ \ $ and $ \ \ v = \sin x $ .

Therefore,

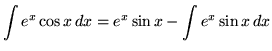$ \displaystyle{ \int {e^x \cos x} \,dx } = \displaystyle{ e^x \sin x - \int{ e^x \sin x } \, dx } $ .

Use integration by parts again. let

$ u = e^x \ \ $ and $ \ \ dv = \sin x \ dx $

so that

$ du = e^x dx \ \ $ and $ \ \ v = -\cos x $ .

Hence,

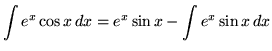
$ \displaystyle{ \int {e^x \cos x} \,dx } = \displaystyle{ e^x \sin x - \int{ e^x \sin x } \, dx } $

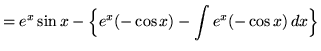
$ = \displaystyle{ e^x \sin x - \Big\{ e^x (-\cos x) - \int{ e^x (-\cos x) } \, dx \Big\} } $

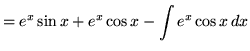$ = \displaystyle{ e^x \sin x + e^x \cos x - \int{ e^x \cos x } \, dx } $ .

To both sides of this "equation" add 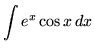$ \displaystyle{ \int { e^x \cos x } \,dx } $ , getting

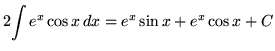$ 2 \displaystyle{ \int { e^x \cos x } \,dx } = \displaystyle{ e^x \sin x + e^x \cos x } + C $ .

Thus,

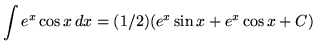
$\displaystyle{ \int { e^x \cos x } \,dx } = (1/2)\displaystyle{( e^x \sin x + e^x \cos x + C ) } $

(Combine constant $ 1/2 $ with $ C $ since $ C $ is an arbitrary constant.)

$ = (1/2)\displaystyle{( e^x \sin x + e^x \cos x) + C } $ .

Click HERE to return to the list of problems.




SOLUTION 23 : Integrate 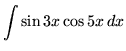$ \displaystyle{ \int{\sin{3x} \cos{5x} } \,dx } $ . Use integration by parts. Let

$ u = \sin{3x} \ \ $ and $ \ \ dv = \cos{5x} \ dx $

so that

$ du = 3 \cos{3x} \ dx \ \ $ and $ \ \ v = (1/5) \sin{5x} $ .

Therefore,

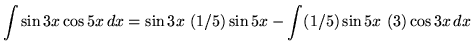
$ \displaystyle{ \int{\sin{3x} \cos{5x} } \,dx } = \displaystyle{ \sin{3x} \ (1/5) \sin{5x} - \int (1/5) \sin{5x} \ (3) \cos{3x} \,dx } $

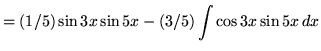$ = \displaystyle{ (1/5) \sin{3x} \sin{5x} - (3/5) \int \cos{3x} \sin{5x} \,dx } $ .

Use integration by parts again. let

$ u = \cos{3x} \ \ $ and $ \ \ dv = \sin{5x} \ dx $

so that

$ du = -3 \sin{3x} \ dx \ \ $ and $ \ \ v = (-1/5) \cos{5x} $ .

Hence,

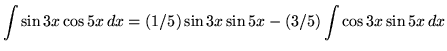
$ \displaystyle{ \int{\sin{3x} \cos{5x} } \,dx } = \displaystyle{ (1/5) \sin{3x} \sin{5x} - (3/5) \int \cos{3x} \sin{5x} \,dx } $

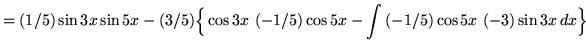
$ = \displaystyle{ (1/5) \sin{3x} \sin{5x} - (3/5) \Big\{ \cos{3x} \ (-1/5) \cos{5x} - \int{ (-1/5) \cos{5x} \ (-3) \sin{3x} } \, dx \Big\} } $

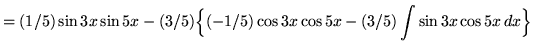
$ = \displaystyle{ (1/5) \sin{3x} \sin{5x} - (3/5) \Big\{ (-1/5) \cos{3x} \cos{5x} - (3/5) \int{ \sin{3x} \cos{5x} } \, dx \Big\} } $

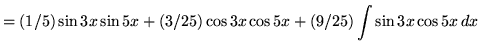$ = \displaystyle{ (1/5) \sin{3x} \sin{5x} + (3/25) \cos{3x} \cos{5x} + (9/25) \int{ \sin{3x} \cos{5x} } \, dx } $ .

From both sides of this "equation" subtract $ (9/25) \int{ \sin{3x} \cos{5x} } \, dx $ , getting

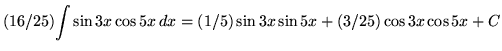$ (16/25) \displaystyle{ \int{\sin{3x} \cos{5x} } \,dx } = \displaystyle{ (1/5) \sin{3x} \sin{5x} + (3/25) \cos{3x} \cos{5x} } + C $ .

Thus,

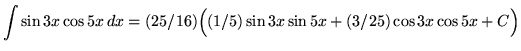
$ \displaystyle{ \int{\sin{3x} \cos{5x} } \,dx } = (25/16) \Big( \displaystyle{ (1/5) \sin{3x} \sin{5x} + (3/25) \cos{3x} \cos{5x} } + C \Big) $

(Combine constant $ 25/16 $ with $ C $ since $ C $ is an arbitrary constant.)

$ = (5/16) \sin{3x} \sin{5x} + (3/16) \cos{3x} \cos{5x} + C $ .

Click HERE to return to the list of problems.




Duane Kouba 2000-04-23