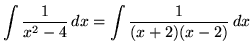
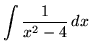Solutions to Integration by Partial Fractions

SOLUTIONS TO INTEGRATION BY PARTIAL FRACTIONS

SOLUTION 1 : Integrate $\displaystyle{ \int { 1 \over x^2 - 4 } \,dx }$ . Factor and decompose into partial fractions, getting

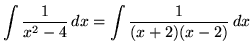
$\displaystyle{ \int { 1 \over x^2 - 4 } \,dx} = \displaystyle{ \int { 1 \over (x+ 2)(x-2)} \,dx}$

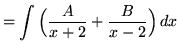
$= \displaystyle{ \int { \Big({A \over x+ 2} + {B \over x-2}\Big)} \,dx}$

(After getting a common denominator, adding fractions, and equating numerators, it follows that $\ \ A(x-2) + B(x+2) = 1$ ;
let $\displaystyle{x = -2: \ A(-4) + B(0) = 1 \longrightarrow A = -\displaystyle{1 \over 4}}$ ;
let $\displaystyle{x = 2: \ A(0) + B(4) = 1 \longrightarrow B = {1 \over 4}}$ .)

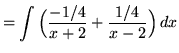
$= \displaystyle{ \int { \Big( {-1/4 \over x+ 2} + {1/4 \over x-2} \Big)} \,dx}$

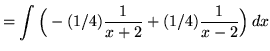
$= \displaystyle{ \int { \Big( -(1/4){1 \over x+2} + (1/4){1 \over x-2} \Big)} \,dx}$

$= \displaystyle{ -{1\over 4} \ln {\vert x+2\vert} + {1\over 4} \ln {\vert x-2\vert} + C}$

$= \displaystyle{ {1\over 4} \Big( \ln \vert x-2\vert - \ln \vert x+2\vert \Big) + C }$

(Recall that $\ \ln m - \ln n = \ln \Big( \displaystyle{ m \over n } \Big)$ .)

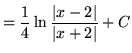$= \displaystyle{ {1\over 4} \ln { \vert x-2\vert \over \vert x+2\vert } + C }$ .

Click HERE to return to the list of problems.

SOLUTION 2 : Integrate 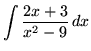$\displaystyle{ \int { 2x + 3 \over x^2 - 9} \,dx }$ . Factor and decompose into partial fractions, getting

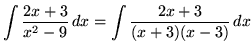
$\displaystyle{ \int { 2x + 3 \over x^2 - 9 } \,dx} = \displaystyle{ \int { 2x+3 \over (x+ 3)(x-3)} \,dx}$

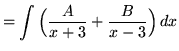
$= \displaystyle{ \int { \Big({A \over x+ 3} + {B \over x-3}\Big)} \,dx}$

(After getting a common denominator, adding fractions, and equating numerators, it follows that $\ \ A(x-3) + B(x+3) = 2x+3$ ;
let $\displaystyle{x = -3: \ A(-6) + B(0) = -3 \longrightarrow A = { 1 \over 2}}$ ;
let $\displaystyle{x = 3: \ A(0) + B(6) = 9 \longrightarrow B = {3 \over 2}}$ .)

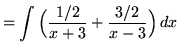
$= \displaystyle{ \int { \Big( {1/2 \over x+ 3} + {3/2 \over x-3} \Big)} \,dx}$

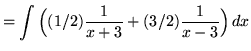
$= \displaystyle{ \int { \Big( (1/2){1 \over x+ 3} + (3/2){1 \over x-3} \Big)} \,dx}$

$= \displaystyle{ {1\over 2} \ln {\vert x+3\vert} + {3\over 2} \ln {\vert x-3\vert} + C}$ .

Click HERE to return to the list of problems.

SOLUTION 3 : Integrate 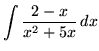$\displaystyle{ \int{ 2 - x \over x^2 + 5x } \,dx }$ . Factor and decompose into partial fractions, getting

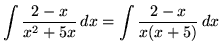
$\displaystyle{ \int { 2 - x \over x^2 + 5x } \,dx} = \displaystyle{ \int { 2-x \over x(x+5)} \,dx}$

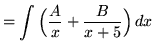
$= \displaystyle{ \int { \Big({A \over x} + {B \over x+5}\Big)} \,dx}$

(After getting a common denominator, adding fractions, and equating numerators, it follows that $\ \ A(x+5) + Bx = 2-x$ ;
let $\displaystyle{x = 0: \ A(5) + B(0) = 2 \longrightarrow A = {2 \over 5}}$ ;
let $\displaystyle{x = -5: \ A(0) + B(-5) = 7 \longrightarrow B = -{7 \over 5}}$ .)

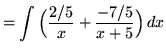
$= \displaystyle{ \int { \Big( { 2/5 \over x} + {-7/5 \over x+5}\Big) } \,dx}$

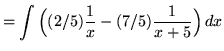
$= \displaystyle{ \int { \Big( (2/5){1 \over x} - (7/5){1 \over x+5}\Big) } \,dx}$

$= \displaystyle{ {2\over 5} \ln {\vert x\vert} - {7\over 5} \ln {\vert x+5\vert} + C }$ .

Click HERE to return to the list of problems.

SOLUTION 4 : Integrate 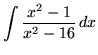$\displaystyle{ \int { x^2 - 1 \over x^2 - 16} \,dx}$ . Because the degree of the numerator is not less than the degree of the denominator, we must first do polynomial division. Then factor and decompose into partial fractions, getting

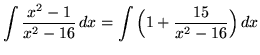
$\displaystyle{ \int { x^2 - 1 \over x^2 - 16 } \,dx } = \displaystyle{ \int { \Big(1 + {15 \over x^2 - 16} \Big) } \,dx }$

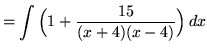
$= \displaystyle{ \int {\Big(1 + {15 \over (x+4)(x-4)} \Big) } \,dx }$

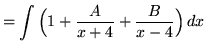
$= \displaystyle{ \int { \Big(1 + {A \over x+4} + { B\over x-4}\Big) } \,dx }$

(After getting a common denominator, adding fractions, and equating numerators, it follows that $\ \ A(x-4) + B(x+4) = 15$ ;
let $\displaystyle{x = -4: \ A(-8) + B(0) = 15 \longrightarrow A = -{15 \over 8}}$ ;
let $\displaystyle{x = 4: \ A(0) + B(8) = 15 \longrightarrow B = {15 \over 8}}$ .)

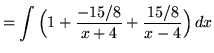
$= \displaystyle{ \int {\Big( 1 + {-15/8 \over x+4} + { 15/8 \over x-4}\Big) } \,dx}$

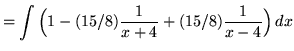
$= \displaystyle{ \int {\Big( 1 - (15/8){1 \over x+4} + (15/8){1 \over x-4}\Big) } \,dx}$

$= \displaystyle{ x -{15\over 8} \ln \vert x+4\vert + {15\over 8} \ln \vert x-4\vert + C}$

$= \displaystyle{ x + {15\over 8} \Big( \ln \vert x-4\vert - \ln \vert x+4\vert \Big) + C }$

(Recall that $\ \ln m - \ln n = \ln \Big( \displaystyle{ m \over n } \Big)$ .)

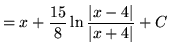$= \displaystyle{ x + {15\over 8} \ln { \vert x-4\vert \over \vert x+4\vert } + C}$ .

Click HERE to return to the list of problems.

SOLUTION 5 : Integrate 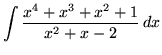$\displaystyle{ \int { x^4 + x^3 + x^2 + 1 \over x^2 + x -2} \,dx }$ . Because the degree of the numerator is not less than the degree of the denominator, we must first do polynomial division. Then factor and decompose into partial fractions, getting

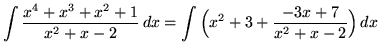
$\displaystyle{ \int { x^4 + x^3 + x^2 + 1 \over x^2 + x -2 } \,dx } = \displaystyle{ \int { \Big(x^2 + 3 + {-3x + 7 \over x^2 + x -2} \Big)} \,dx }$

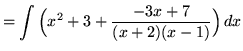
$= \displaystyle{ \int { \Big(x^2 + 3 + {-3x + 7 \over (x+2)(x-1)}\Big) } \,dx }$

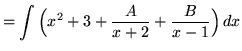
$= \displaystyle{ \int { \Big(x^2 + 3 + {A \over x+2} + {B \over x-1} \Big) } \,dx }$

(After getting a common denominator, adding fractions, and equating numerators, it follows that $\ \ A(x-1) + B(x+2) = -3x + 7$ ;
let $\displaystyle{x = -2: \ A(-3) + B(0) = 13 \longrightarrow A = -{13 \over 3}}$ ;
let $\displaystyle{x = 1: \ A(0) + B(3) = 4 \longrightarrow B = {4 \over 3}}$ .)

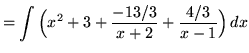
$= \displaystyle{ \int{ \Big( x^2 + 3 + {-13/3 \over x+2} + {4/3 \over x-1} \Big)} \,dx}$

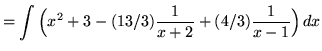
$= \displaystyle{ \int{ \Big( x^2 + 3 - (13/3) {1 \over x+2} + (4/3){1 \over x-1} \Big)} \,dx}$

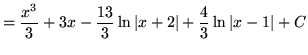$= \displaystyle{ {x^3 \over 3} +3x -{13\over 3} \ln {\vert x+2\vert} + {4\over 3} \ln {\vert x-1\vert} + C}$ .

Click HERE to return to the list of problems.

SOLUTION 6 : Integrate 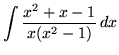$\displaystyle{ \int {x^2 + x - 1 \over x(x^2 - 1) } \,dx }$ . Factor and decompose into partial fractions, getting

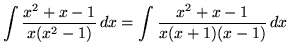
$\displaystyle{ \int {x^2 + x - 1 \over x(x^2 - 1) } \,dx } = \displaystyle{ \int { x^2 + x - 1 \over x(x+1)(x - 1) } \,dx }$

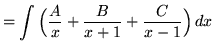
$= \displaystyle{ \int { \Big( {A \over x} + {B \over x+1} + {C \over x-1}\Big) } \,dx }$

(After getting a common denominator, adding fractions, and equating numerators, it follows that

;

let $\displaystyle{x = 0: \ A(-1) + B(0) + C(0) = -1 \longrightarrow A = 1}$ ;
let $\displaystyle{x = -1: \ A(0) + B(2) + C(0) = -1 \longrightarrow B = -{1 \over 2}}$ ;
let $\displaystyle{x = 1: \ A(0) + B(0) + C(2) = 1 \longrightarrow C = {1 \over 2}}$ .)

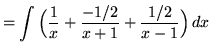
$= \displaystyle{ \int { \Big({1 \over x} + {-1/2\over x+1} + {1/2 \over x-1} \Big) } \,dx}$

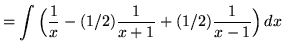
$= \displaystyle{ \int { \Big({1 \over x} - (1/2) {1\over x+1} + (1/2) {1 \over x-1} \Big) } \,dx}$

$= \displaystyle{ \ln \vert x\vert -{1\over 2} \ln {\vert x+1\vert} + {1\over 2} \ln {\vert x-1\vert} + C}$

$= \displaystyle{ \ln \vert x\vert + {1\over 2} \Big( \ln \vert x-1\vert - \ln \vert x+1\vert \Big) + C }$

(Recall that $\ \ln m - \ln n = \ln \Big( \displaystyle{ m \over n } \Big)$ .)

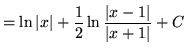$= \displaystyle{ \ln \vert x\vert + {1\over 2} \ln { \vert x-1\vert \over \vert x+1\vert } + C }$ .

Click HERE to return to the list of problems.

SOLUTION 7 : Integrate 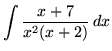$\displaystyle{ \int { x + 7 \over x^2(x+2) } \,dx }$ . Decompose into partial fractions (There is a repeated linear factor !), getting

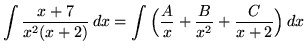
$\displaystyle{ \int { x + 7 \over x^2(x+2) } \,dx} = \displaystyle{ \int {\Big( {A \over x} + {B \over x^2} + {C \over x+2}\Big) } \,dx}$

(After getting a common denominator, adding fractions, and equating numerators, it follows that $\ \ Ax(x+2) + B(x+2) + Cx^2 = x+7$ ;
let $\displaystyle{x = 0: \ A(0) + B(2) + C(0) = 7 \longrightarrow B = {7 \over 2}}$ ;
let $\displaystyle{x = -2: \ A(0) + B(0) + C(4) = 5 \longrightarrow C = {5 \over 4}}$ ;
let $\displaystyle{x = -1: \ A(-1) + B(1) + C(1) = -A + {7 \over 2} + {5 \over 4} = 6 \longrightarrow A = -{5 \over 4} }$ .)

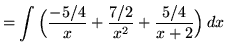
$= \displaystyle{ \int {\Big({-5/4 \over x} + {7/2 \over x^2} + {5/4 \over x+2} \Big) } \,dx}$

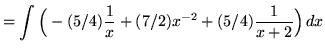
$= \displaystyle{ \int {\Big( -(5/4){1 \over x} + (7/2)x^{-2} + (5/4){1 \over x+2} \Big) } \,dx}$

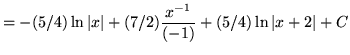
$= \displaystyle{ -(5/4) \ln \vert x\vert + (7/2) {x^{-1} \over (-1)} + (5/4) \ln \vert x+2\vert + C }$

$= \displaystyle{ -{5 \over 4} \ln \vert x\vert - {7 \over 2x} + {5 \over 4} \ln \vert x+2\vert + C }$ .

Click HERE to return to the list of problems.

SOLUTION 8 : Integrate 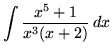$\displaystyle{ \int {x^5 + 1 \over x^3(x+2) } \,dx }$ . Because the degree of the numerator is not less than the degree of the denominator, we must first do polynomial division. Then factor and decompose into partial fractions (There is a repeated linear factor !), getting

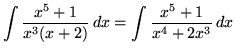
$\displaystyle{ \int {x^5 + 1 \over x^3(x+2)} \,dx } = \displaystyle{ \int {x^5 + 1 \over x^4+2x^3 } \,dx }$

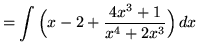
$= \displaystyle{ \int {\Big( x - 2 + {4x^3 + 1 \over x^4+2x^3 }\Big) } \,dx }$

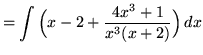
$= \displaystyle{ \int {\Big( x - 2 + {4x^3 + 1 \over x^3(x+2) }\Big) } \,dx }$

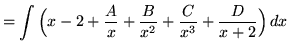
$= \displaystyle{ \int { \Big( x - 2 + {A \over x} + { B \over x^2} + { C \over x^3} + { D \over x+2}\Big)} \,dx }$

(After getting a common denominator, adding fractions, and equating numerators, it follows that

;

let $\displaystyle{x = 0: \ A(0) + B(0) + C(2) + D(0) = 1 \longrightarrow C = {1 \over 2}}$ ;
let $\displaystyle{x = -2: \ A(0) + B(0) + C(0) + D(-8) = -31 \longrightarrow D = {31 \over 8}}$ ;
let $\displaystyle{x = 1: \ A(3) + B(3) + C(3) + D = 3A + 3B + {3 \over 2} + {31 \over 8} = 5 }$
$\ \ \ \ \ \ \ \ \displaystyle{\longrightarrow A + B = -{1 \over 8}}$ ;
let $\displaystyle{x = -1: \ A(1) + B(1) + C(1) + D(-1) = A - B + {1 \over 2} - {31 \over 8} = -3 }$
$\ \ \ \ \ \ \ \ \displaystyle{ \longrightarrow A - B = {3 \over 8}}$ ;
it follows that $\ A = \displaystyle{1 \over 8}$ and $B = -\displaystyle{1 \over 4}$ .)

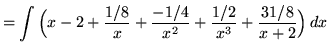
$= \displaystyle{ \int { \Big( x - 2 + {1/8 \over x} + { -1/4 \over x^2} + { 1/2 \over x^3} + { 31/8 \over x+2} \Big) } \,dx }$

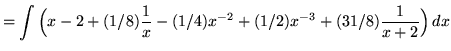
$= \displaystyle{ \int { \Big( x - 2 + (1/8){1 \over x} - (1/4)x^{-2} + (1/2)x^{-3} + (31/8){1 \over x+2}\Big) } \, dx }$

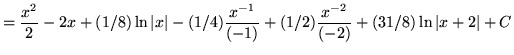
$= \displaystyle{ {x^2 \over 2} - 2x + (1/8) \ln \vert x\vert -(1/4){ x^{-1} \over (-1)}+ (1/2){ x^{-2} \over (-2) } + (31/8) \ln \vert x+2\vert +C }$

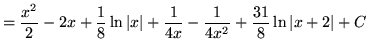$= \displaystyle{ {x^2 \over 2} - 2x + {1 \over 8} \ln \vert x\vert + {1\over 4x} - {1\over 4x^2} + {31 \over 8} \ln \vert x+2\vert + C }$ .

Click HERE to return to the list of problems.

About this document ...

Duane Kouba 2000-05-02