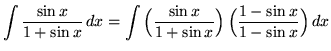
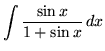Next: About this document ...

SOLUTIONS TO U-SUBSTITUTION



SOLUTION 10 : Integrate $ \displaystyle{ \int {\sin x \over 1 + \sin x } \,dx } $ . First rewrite the function by multiplying by 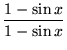$ \displaystyle{ 1 - \sin x \over 1 - \sin x } $ , getting

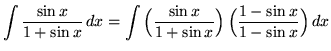
$ \displaystyle{ \int {{\sin x \over 1 + \sin x } } \,dx } = \displaystyle{ \i... ... \over 1 + \sin x } \Big) \, \Big( { 1 -\sin x \over 1 - \sin x} }\Big) \,dx } $

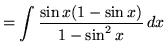
$ = \displaystyle{ \int {{\sin x (1 - \sin x) \over 1 - \sin^2 x } } \,dx }$

(In the denominator use trig identity A from the beginning of this section.)

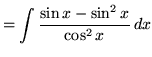
$ = \displaystyle{ \int {\sin x - \sin^2 x \over \cos^2 x } \,dx }$

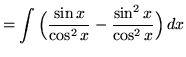
$ = \displaystyle{ \int {\Big({\sin x \over \cos^2 x} - {\sin^2 x \over \cos^2 x }\Big) } \,dx }$

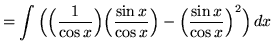
$ = \displaystyle{ \int {\Big(\Big({1 \over \cos x}\Big)\Big({\sin x \over \cos x}\Big) - \Big( {\sin x \over \cos x }\Big)^2 } \Big) \,dx }$

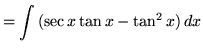
$ = \displaystyle{ \int {({ \sec x \tan x } - \tan^2 x) } \,dx }$

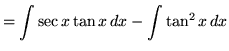
$ = \displaystyle{ \int \sec x \tan x \,dx - \int \tan^2 x \,dx }$

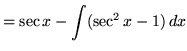
(Use antiderivative rule 5 and trig identity F from the beginning of this section.) truein $ = \sec x - \displaystyle{ \int ( \sec^2 x - 1) \,dx }$

$ = \displaystyle{ \sec x - ( \tan x - x ) + C} $

$ = \displaystyle{ \sec x - \tan x + x + C} $ .

Click HERE to return to the list of problems.




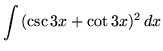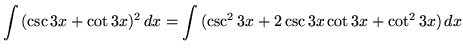
SOLUTION 11 : Integrate $ \displaystyle{ \int {(\csc {3x} + \cot{3x})^2 } \,dx } $ . First square the function, getting truein $ \displaystyle{ \int {(\csc {3x} + \cot{3x})^2 } \,dx} =\displaystyle{ \int{( \csc ^2 {3x} + 2\csc{3x}\cot{3x} + \cot^2{3x})}\,dx} $

(Use trig identity G from the beginning of this section.)

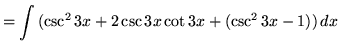
$ = \displaystyle{ \int{( \csc ^2 {3x} + 2\csc{3x}\cot{3x} + (\csc^2{3x} - 1) )}\,dx} $

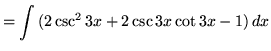
$ = \displaystyle{ \int{( 2 \csc ^2 {3x} + 2\csc{3x}\cot{3x} - 1 )}\,dx} $

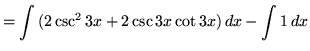
$ = \displaystyle{ \int{( 2 \csc ^2 {3x} + 2\csc{3x}\cot{3x} )}\,dx - \int 1 \,dx } $

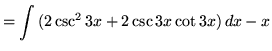$ = \displaystyle{ \int{( 2 \csc ^2 {3x} + 2\csc{3x}\cot{3x} )}\,dx} - x $ .

Now use u-substitution. Let

$ u = 3x $

so that

$ du = 3 dx $ ,

or

$ (1/3) du = dx $ .

Substitute into the original problem, replacing all forms of $ x $, getting

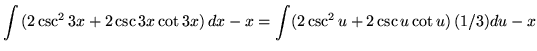
$ \displaystyle{ \int{( 2 \csc ^2 {3x} + 2\csc{3x}\cot{3x} )}\,dx} - x = \displaystyle{ \int (2 \csc ^2 u + 2 \csc u \cot u) \,(1/3)du } - x $

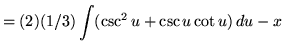
$ = \displaystyle{ (2)(1/3) \int (\csc ^2 u + \csc u \cot u ) \,du } - x $

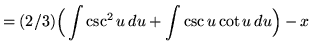
$ = \displaystyle{ (2/3) \Big( \int \csc ^2 u \, du + \int \csc u \cot u \, du} \Big) - x $

(Use antiderivative rule 4 on the first integral. Use antiderivative rule 6 on the second integral.)

$ = \displaystyle{ (2/3)( (- \cot u) + (- \csc u) + C ) } - x $

(Combine constant $ 2/3 $ with $ C $ since $ C $ is an arbitrary constant.)

$ = \displaystyle{ (-2/3) \cot u - (2/3) \csc u - x + C } $

$ = \displaystyle{ (-2/3) \cot 3x - (2/3) \csc 3x - x + C } $ .

Click HERE to return to the list of problems.




SOLUTION 12 : Integrate 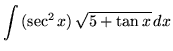$ \displaystyle{ \int { (\sec^2 x) \, \sqrt{ 5 + \tan x} } \,dx } $. Use u-substitution. Let

$ u = 5 + \tan x $

so that

$ du = \displaystyle{ \sec^2 x } \ dx $ .

Substitute into the original problem, replacing all forms of $ x $, getting

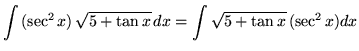
$ \displaystyle{ \int { (\sec^2 x) \, \sqrt{ 5 + \tan x} } \,dx } = \displaystyle{ \int { \sqrt{ 5 + \tan x} } \, (\sec^2 x)dx } $

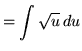
$ = \displaystyle{ \int { \sqrt {u}} \, du } $

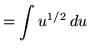
$ = \displaystyle{ \int { u^{1/2} } \, du } $

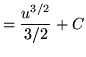
$ = \displaystyle{ {u^{3/2} \over 3/2} + C } $

$ = \displaystyle{ {2 \over 3} (5 + \tan x)^{3/2} + C } $ .

Click HERE to return to the list of problems.




SOLUTION 13 : Integrate 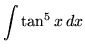$ \displaystyle{ \int \tan^5 x \,dx } $. First rewrite the function (Recall that $ A^m A^n = A^{m+n} $ .), getting

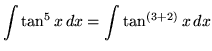
$ \displaystyle{ \int \tan^5 x \, dx } = \displaystyle{ \int \tan^{(3+2)} x \,dx } $

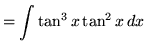
$ = \displaystyle{ \int \tan^3 x \tan^2 x \, dx } $

(Now use trig identity F from the beginning of this section.)

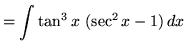
$ = \displaystyle{ \int \tan^3 x \ (\sec^2 x - 1) \, dx } $

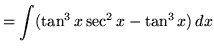
$ = \displaystyle{ \int ( \tan^3 x \sec^2 x - \tan^3 x ) \, dx } $

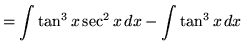$ = \displaystyle{ \int \tan^3 x \sec^2 x \, dx - \int \tan^3 x \, dx } $ .

On the first integral use u-substitution. Rewrite the second integral and use trig identity F again. Let

$ u = \tan x $

so that

$ du = \sec^2 x \ dx $ .

Substitute into the original problem, replacing all forms of $ x $, getting

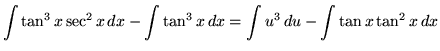
$ \displaystyle{ \int \tan^3 x \sec^2 x \, dx - \int \tan^3 x \, dx } = \displaystyle{ \int u^3 \, du - \int \tan x \tan^2 x \, dx } $

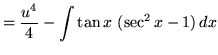
$ = \displaystyle{ { u^4 \over 4 } - \int \tan x \ (\sec^2 x - 1) \, dx } $

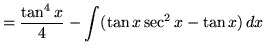
$ = \displaystyle{ { \tan^4 x \over 4 } - \int (\tan x \sec^2 x - \tan x) \, dx } $

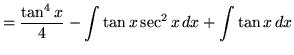$ = \displaystyle{ { \tan^4 x \over 4 } - \int \tan x \sec^2 x \, dx + \int \tan x \, dx } $ .

Use u-substitution on the first integral. Use antiderivative rule 7 on the second integral. Let

$ u = \tan x $

so that

$ du = \sec^2 x \ dx $ .

Substitute into the original problem, replacing all forms of $ x $, getting

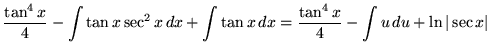
$ \displaystyle{ { \tan^4 x \over 4 } - \int \tan x \sec^2 x \, dx + \int \tan x... ...\displaystyle{ { \tan^4 x \over 4 } - \int u \, du + \ln\vert \sec x \vert } $

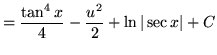
$ = \displaystyle{ { \tan^4 x \over 4 } - { u^2 \over 2 } + \ln\vert \sec x \vert } + C $

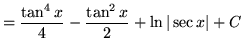$ = \displaystyle{ { \tan^4 x \over 4 } - { \tan^2 x \over 2 } + \ln\vert \sec x \vert } + C $ .

Click HERE to return to the list of problems.




SOLUTION 14 : Integrate 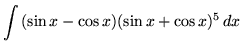$ \displaystyle{ \int { (\sin x - \cos x) (\sin x + \cos x)^5 } \,dx } $. Use u-substitution. Let

$ u = \sin x + \cos x $

so that

$ du = (\cos x - \sin x) dx = -(\sin x - \cos x) dx $ ,

or

$ (-1) du = (\sin x - \cos x) dx $ .

Substitute into the original problem, replacing all forms of $ x $, getting

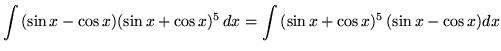
$ \displaystyle{ \int {(\sin x - \cos x) (\sin x + \cos x)^5 } \,dx } = \displaystyle{ \int { (\sin x + \cos x)^5 } \,(\sin x - \cos x) dx } $

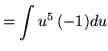
$ = \displaystyle{ \int { u^5} \, (-1)du } $

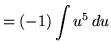
$ = \displaystyle{ (-1) \int { u^5} \, du } $

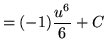
$ = \displaystyle{ (-1) { u^6 \over 6 } + C } $

$ = \displaystyle{ -(1/6) {( \sin x + \cos x)^6 } + C } $ .

Click HERE to return to the list of problems.




SOLUTION 15 : Integrate 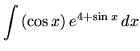$ \displaystyle{ \int{ (\cos x) \, e^{4+\sin x} } \,dx } $. Let

$ u = 4 + \sin x $

so that

$ du = \cos x \ dx $ .

Substitute into the original problem, replacing all forms of $ x $, getting

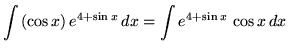
$ \displaystyle{ \int {( \cos x ) \, e^{4+\sin x} } \,dx } = \displaystyle{ \int { e^{4+\sin x} } \, \cos x \, dx } $

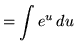
$ = \displaystyle{ \int { e^u } \, du } $

$ = \displaystyle{ e^u + C } $

$ = \displaystyle{ e^{4+\sin x} + C } $ .

Click HERE to return to the list of problems.




SOLUTION 16 : Integrate 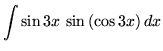$ \displaystyle{ \int{\sin{3x} \, \sin{(\cos{3x})} } \,dx } $ . (Hello ! The term $ \sin{(\cos{3x})} $ is NOT the product of $ \sin $ and $ \cos{3x} $ . It is the functional composition of functions $ \sin x $ and $ \cos{3x} $ . ) Use u-substitution. Let

$u = \cos{3x} $

so that

$ du = -3 \sin{3x} \ dx $ ,

or

$ (-1/3) du = \sin{3x} \ dx $ .

Substitute into the original problem, replacing all forms of $ x $, getting

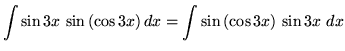
$ \displaystyle{\int{\sin{3x} \, \sin{(\cos{3x})} } \,dx } = \displaystyle{\int{ \sin{(\cos{3x})} } \, \sin{3x} \ dx } $

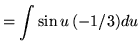
$ = \displaystyle{ \int{ \sin u }\, (-1/3)du} $

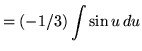
$ = \displaystyle{ (-1/3) \int{ \sin u }\, du} $

$ = -(1/3)\displaystyle{ (-\cos u) + C } $

$ = (1/3) \cos u + C $

$ = (1/3)\displaystyle{ \cos{(\cos{3x})} + C} $ .

Click HERE to return to the list of problems.




SOLUTION 17 : Integrate 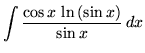$ \displaystyle{ \int{\cos{x} \,\ln{(\sin x)} \over \sin x } \,dx } $ . Use u-substitution. Let

$ u = \ln{(\sin x)} $

so that

$ du =\displaystyle{ {1 \over \sin x} \cos x} \ dx = \displaystyle{ \cos x \over \sin x } \ dx $ .

Substitute into the original problem, replacing all forms of $ x $, getting

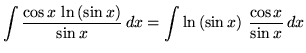
$ \displaystyle{\int{ \cos{x} \,\ln{(\sin x)} \over \sin x} \,dx } = \displaystyle{\int{ \ln{(\sin x)} \ { \cos{x}\over \sin x } } \,dx } $

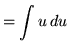
$ = \displaystyle{ \int{ u } \, du} $

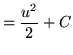
$ = \displaystyle{ {u^2 \over 2} + C } $

$ = \displaystyle{ {1\over 2} (\ln{(\sin x)})^2 + C} $ .

Click HERE to return to the list of problems.




SOLUTION 18 : Integrate 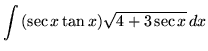$ \displaystyle{ \int{(\sec x \tan x) \sqrt{4 + 3 \sec x}} \,dx } $ . Use u-substitution. Let

$ u = 4 + 3 \sec x $

so that

$ du = 3 \sec x \tan x \ dx $ ,

or

$ (1/3)du = \sec x \tan x \ dx $ .

Substitute into the original problem, replacing all forms of $ x $, getting

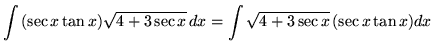
$ \displaystyle{\int{(\sec x \tan x) \sqrt{4 + 3 \sec x} } \,dx } = \displaystyle{\int{ \sqrt{4 + 3 \sec x} } \,(\sec x \tan x) dx } $

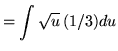
$ = \displaystyle{ \int{ \sqrt{u} }\, (1/3)du} $

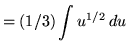
$ = \displaystyle{ (1/3) \int{ u^{1/2} }\, du} $

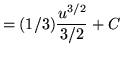
$ = \displaystyle{ (1/3){u^{3/2} \over 3/2} + C } $

$ = \displaystyle{ {2\over 9} ( 4 + 3 \sec x )^{3/2} + C } $ .

Click HERE to return to the list of problems.





Next: About this document ...

Duane Kouba 2000-04-19