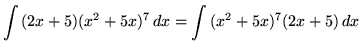
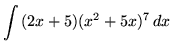Next: About this document ...

SOLUTIONS TO U-SUBSTITUTION



SOLUTION 1 : Integrate $ \displaystyle{ \int { (2x+5) (x^2+5x)^7 } \,dx } $ . Let

u = x2+5x

so that

du = (2x+5) dx .

Substitute into the original problem, replacing all forms of x, getting

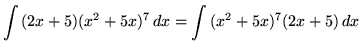
$ \displaystyle{ \int { (2x+5) (x^2+5x)^7 } \,dx } = \displaystyle{ \int { (x^2+5x)^7 (2x+5) } \,dx } $

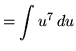
$ = \displaystyle{ \int { u^7 } \,du } $

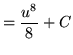
$ = \displaystyle{ { u^8 \over 8 } + C } $

$ = \displaystyle{ {(1/8)(x^2+5x)^8 } + C } $ .

Click HERE to return to the list of problems.




SOLUTION 2 : Integrate 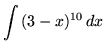$ \displaystyle{ \int { (3-x)^{10} } \,dx } $ . Let

u = 3-x

so that

du = (-1) dx ,

or

(-1) du = dx .

Substitute into the original problem, replacing all forms of x, getting

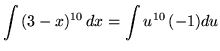
$ \displaystyle{ \int { (3-x)^{10} } \,dx } = \displaystyle{ \int { u^{10} } \,(-1)du } $

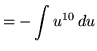
$ = \displaystyle{ - \int { u^{10} } \,du } $

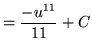
$ = \displaystyle{ { - u^{11} \over 11 } + C } $

$ = \displaystyle{ { (-1/11) (3-x)^{11} } + C } $ .

Click HERE to return to the list of problems.




SOLUTION 3 : Integrate 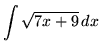$ \displaystyle{ \int \sqrt{ 7x+9 } \,dx } $ . Let

u = 7x+9

so that

du = 7 dx ,

or

(1/7) du = dx .

Substitute into the original problem, replacing all forms of x, getting

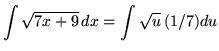
$ \displaystyle{ \int { \sqrt{ 7x+9 }} \,dx } = \displaystyle{ \int {\sqrt{ u }} \,(1/7)du } $

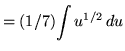
$ = (1/7) \displaystyle{ \int { u^{1/2} } \,du } $

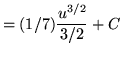
$ = \displaystyle{ (1/7){ u^{3/2} \over {3/2} } + C } $

$ = \displaystyle{ (1/7)(2/3)(7x+9)^{3/2} + C } $

$ = \displaystyle{ (2/21)(7x+9)^{3/2} + C } $ .

Click HERE to return to the list of problems.




SOLUTION 4 : Integrate 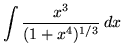$ \displaystyle{ \int { x^3 \over (1+x^4)^{1/3} } \,dx } $ . Let

u = 1+x4

so that

du = 4x3 dx ,

or

(1/4) du = x3 dx .

Substitute into the original problem, replacing all forms of x, getting

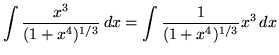
$ \displaystyle{ \int { x^3 \over (1+x^4)^{1/3} } \,dx } = \displaystyle{ \int { 1 \over (1+x^4)^{1/3} } x^3 \,dx } $

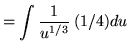
$ = \displaystyle{ \int { 1 \over u^{1/3} } \,(1/4) du } $

(Do not make the following VERY COMMON MISTAKE : 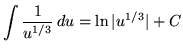$ \displaystyle{ \int { 1 \over u^{1/3} } \, du } = \displaystyle{ \ln \vert u^{1/3} \vert } + C $ . Why is this INCORRECT ?)

$ = (1/4) \displaystyle{ \int { u^{-1/3} } \, du } $

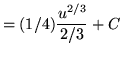
$ = (1/4) \displaystyle{ { u^{2/3} \over {2/3} } + C } $

$ = \displaystyle{ (1/4)(3/2)(1+x^4)^{2/3} + C } $

$ = \displaystyle{ (3/8)(1+x^4)^{2/3} + C } $ .

Click HERE to return to the list of problems.




SOLUTION 5 : Integrate 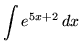$ \displaystyle{ \int { e^{5x+2} } \,dx } $ . Let

u = 5x+2

so that

du = 5 dx ,

or

(1/5) du = dx .

Substitute into the original problem, replacing all forms of x, getting

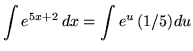
$ \displaystyle{ \int { e^{5x+2} } \,dx } = \displaystyle{ \int { e^{u} } \,(1/5)du } $

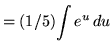
$ = (1/5) \displaystyle{ \int { e^u } \, du } $

$ = (1/5) \displaystyle{ { e^u } + C } $

$ = (1/5) \displaystyle{ { e^{5x+2} } + C } $ .

Click HERE to return to the list of problems.




SOLUTION 6 : Integrate 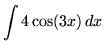$ \displaystyle{ \int { 4 \cos(3x) } \,dx } $ . Let

u = 3x

so that

du = 3 dx ,

or

(1/3) du = dx .

Substitute into the original problem, replacing all forms of x, getting

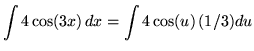
$ \displaystyle{ \int { 4 \cos(3x) } \,dx } = \displaystyle{ \int { 4 \cos(u) } \,(1/3)du } $

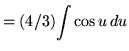
$ = (4/3) \displaystyle{ \int { \cos u } \, du } $

$ = (4/3) \displaystyle{ { \sin u } + C } $

$ = (4/3) \displaystyle{ { \sin(3x) } + C } $ .

Click HERE to return to the list of problems.




SOLUTION 7 : Integrate 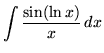$ \displaystyle{ \int { \sin( \ln x ) \over x } \,dx } $ . Let

$ u = \ln x $

so that

$ du = \displaystyle{ 1 \over x } dx $ .

Substitute into the original problem, replacing all forms of x, getting

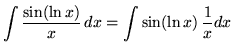
$ \displaystyle{ \int { \sin( \ln x ) \over x } \,dx } = \displaystyle{ \int \sin( \ln x ) \,{ 1 \over x } dx } $

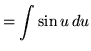
$ = \displaystyle{ \int { \sin u } \, du } $

$ = \displaystyle{ { -\cos u } + C } $

$ = \displaystyle{ { -\cos(\ln x) } + C } $ .

Click HERE to return to the list of problems.




Duane Kouba
1999-05-07