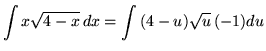
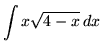Solutions to U-Substitution

Next: About this document ...

SOLUTIONS TO U-SUBSTITUTION

SOLUTION 14 : Integrate $\displaystyle{ \int { x \sqrt{4-x} } \,dx }$ . Let

u = 4-x

so that

du = (-1) dx ,

(-1) du = dx .

In addition, we can "back substitute" with

x = 4-u .

Substitute into the original problem, replacing all forms of x, getting

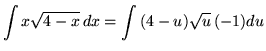
$\displaystyle{ \int { x \sqrt{4-x} } \,dx } = \displaystyle{ \int { (4-u) \sqrt{u} } \,(-1) du }$

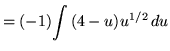
$= (-1) \displaystyle{ \int { (4-u) u^{1/2} } \, du }$

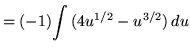
$= (-1) \displaystyle{ \int { (4 u^{1/2} - u^{3/2} ) } \,du }$

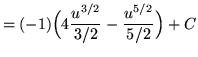
$= (-1) \Big( \displaystyle{ 4 { u^{3/2} \over {3/2} } - { u^{5/2} \over {5/2} } \Big)+ C }$

$= \displaystyle{ -4 (2/3) u^{3/2} + (2/5) u^{5/2} + C }$

$= \displaystyle{ (2/5) (4-x)^{5/2} - (8/3) (4-x)^{3/2} + C }$ .

Click HERE to return to the list of problems.

SOLUTION 15 : Integrate 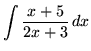$\displaystyle{ \int { x+5 \over 2x+3 } \,dx }$ . Let

u = 2x+3

so that

du = 2 dx ,

(1/2) du = dx .

In addition, we can "back substitute" with

x = (1/2)(u-3) .

Substitute into the original problem, replacing all forms of x, getting

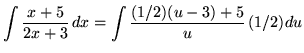
$\displaystyle{ \int { x+5 \over 2x+3 } \,dx } = \displaystyle{ \int { (1/2)(u-3)+5 \over u } \,(1/2) du }$

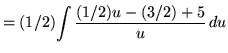
$= (1/2) \displaystyle{ \int { (1/2)u-(3/2)+5 \over u } \, du }$

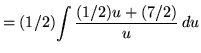
$= (1/2) \displaystyle{ \int { (1/2)u+(7/2) \over u } \, du }$

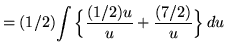
$= (1/2) \displaystyle{ \int \Big\{ { (1/2)u \over u } + { (7/2) \over u } \Big\} \, du }$

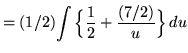
$= (1/2) \displaystyle{ \int \Big\{ { 1 \over 2 } + { (7/2) \over u } \Big\} \, du }$

$= (1/2) \Big\{ \displaystyle{ (1/2)u + (7/2) \ln \vert u\vert } \Big\} + C$

$= \displaystyle{ (1/4)u + (7/4) \ln \vert u\vert } + C$

$= \displaystyle{ (1/4)(2x+3) + (7/4) \ln \vert 2x+3\vert } + C$ .

Click HERE to return to the list of problems.

SOLUTION 16 : Integrate 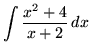$\displaystyle{ \int { x^2+4 \over x+2 } \,dx }$ . Let

u = x+2

so that

du = (1) dx = dx .

In addition, we can "back substitute" with

x = u-2 .

Substitute into the original problem, replacing all forms of x, getting

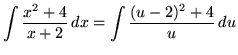
$\displaystyle{ \int { x^2+4 \over x+2 } \,dx } = \displaystyle{ \int { (u-2)^2+4 \over u } \, du }$

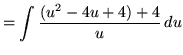
$= \displaystyle{ \int { (u^2-4u+4)+4 \over u } \, du }$

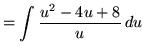
$= \displaystyle{ \int { u^2-4u+8 \over u } \, du }$

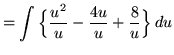
$= \displaystyle{ \int \Big\{ { u^2 \over u } - {4u \over u } + { 8 \over u } \Big\}\, du }$

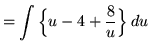
$= \displaystyle{ \int \Big\{ u - 4 + { 8 \over u } \Big\}\, du }$

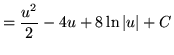
$= \displaystyle{ { u^2 \over 2 } - 4u + 8 \ln \vert u\vert } + C$

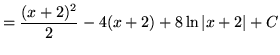$= \displaystyle{ { (x+2)^2 \over 2 } - 4(x+2) + 8 \ln \vert x+2\vert } + C$ .

Click HERE to return to the list of problems.

SOLUTION 17 : Integrate 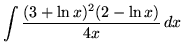$\displaystyle{ \int { (3 + \ln x)^2 (2 - \ln x) \over 4x } \,dx }$ . Let

$u = 3 + \ln x$

so that

$du = \displaystyle{ 1 \over x } dx$ .

In addition, we can "back substitute" with

$\ln x = u-3$ .

Substitute into the original problem, replacing all forms of x, getting

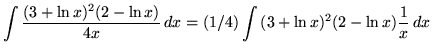
$\displaystyle{ \int { (3 + \ln x)^2 (2 - \ln x) \over 4x } \,dx } = \displaystyle{ (1/4) \int { (3 + \ln x)^2 (2 - \ln x) } { 1 \over x } \,dx }$

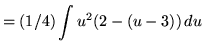
$= \displaystyle{ (1/4) \int { u^2 (2 - ( u-3 )) } \,du }$

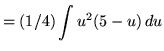
$= \displaystyle{ (1/4) \int { u^2 ( 5-u ) } \,du }$

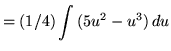
$= \displaystyle{ (1/4) \int { (5 u^2 - u^3 ) } \,du }$

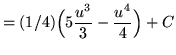
$= \displaystyle{ (1/4) \Big( 5 { u^3 \over 3 } - { u^4 \over 4 } \Big) } + C$

$= \displaystyle{ (5/12)u^3 - (1/16) u^4 } + C$

$= \displaystyle{ (5/12)(3 + \ln x)^3 - (1/16) (3 + \ln x)^4 } + C$ .

Click HERE to return to the list of problems.

SOLUTION 18 : Integrate 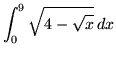$\displaystyle{ \int_{0}^{9} \sqrt{ 4 - \sqrt{ x } } \,dx }$ . Let

$u = 4 - \sqrt{ x }$ .

In addition, we can "back substitute" with

$\sqrt{ x } = 4-u$ ,

x = (4-u)² = u²-8u+16 .

Then

dx = (2u-8) du .

In addition, the range of x-values is

$x : 0 \longrightarrow 9$ ,

so that the range of u-values is

$u : ( 4 - \sqrt{0} ) \longrightarrow ( 4 - \sqrt{9} )$ ,

$u : 4 \longrightarrow 1$ .

Substitute into the original problem, replacing all forms of x, getting

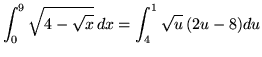
$\displaystyle{ \int_{0}^{9} \sqrt{ 4 - \sqrt{ x } } \,dx } = \displaystyle{ \int_{4}^{1} \sqrt{ u } \, (2u-8) du }$

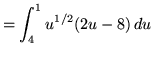
$= \displaystyle{ \int_{4}^{1} { u }^{1/2} (2u-8) \, du }$

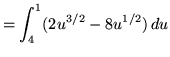
$= \displaystyle{ \int_{4}^{1} ( 2u^{3/2} -8u^{1/2}) \, du }$

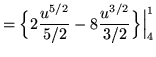
$= \displaystyle{ \Big\{ 2 { u^{5/2} \over 5/2 } - 8 { u^{3/2} \over 3/2 } \Big\} \Big\vert_{4}^{1} }$

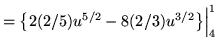
$= \displaystyle{ \big\{ 2(2/5) u^{5/2} - 8(2/3) u^{3/2} \big\} \Big\vert_{4}^{1} }$

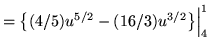
$= \displaystyle{ \big\{ (4/5) u^{5/2} - (16/3) u^{3/2} \big\} \Big\vert_{4}^{1} }$

$= \displaystyle{ \big\{ (4/5) (1)^{5/2} - (16/3) (1)^{3/2} \big\} - \big\{ (4/5) (4)^{5/2} - (16/3) (4)^{3/2} \big\} }$

$= \displaystyle{ \Big\{ { 4 \over 5 } (1) - { 16 \over 3 } (1) \Big\} - \Big\{ { 4 \over 5 } (32) - { 16 \over 3 } (8) \Big\} }$

$= \displaystyle{ \Big\{ { 4 \over 5 } - { 128 \over 5 } \Big\} + \Big\{ { 128 \over 3 } - { 16 \over 3 } \Big\} }$

$= \displaystyle{ { -124 \over 5 } + { 122 \over 3 } }$

$= \displaystyle{ { 610 - 372 \over 15 } }$

$= \displaystyle{ { 238 \over 15 } }$ .

Click HERE to return to the list of problems.

About this document ...

Duane Kouba
1999-05-07