|
|
Introduction to Lattice Points
Introduction
Suppose we are given a Polygon P inscribed on a grid with squares of unit length in
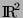 . Now, define a lattice point to be
an integer coordinate point lying on such a grid. Refer to figures 1 and 2 for examples of the above. . Now, define a lattice point to be
an integer coordinate point lying on such a grid. Refer to figures 1 and 2 for examples of the above.
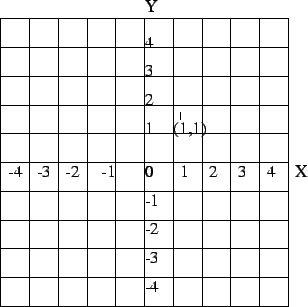
Figure:
(1,1) denotes a lattice point
|
|
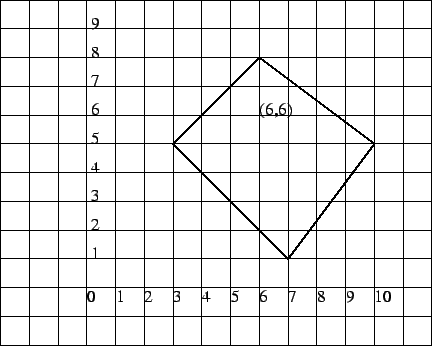
Figure:
a polygon P inscribed on a grid in
|
|
A natural question arises, how many lattice points lie inside and on the boundary of a given polygon P?
We can explore this question by first experimenting with circles. Indeed according to, Karl Friedrich Gauss, given
a circle of radius r
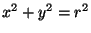 s.t. r 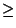 1
the number of lattice points that lie on the boundary and inside the circle is related to the
area of the circle. i.e.,
the accompanying error function is as follows:
Interestingly enough the exact value of 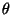 is not known.
If we let G(r) denote the number of lattice points that lie inside and on the boundary of a given circle,
Gauss calculated that: G(1) = 5 G(2) = 13 G(3) = 29 G(4) = 49 G(5) = 81 G(6) = 113 G(7) = 149 . . . G(30) = 2821 . . . G(300) = 282,697,
Gauss cared because the function G(r) can be used to approximate is not known.
If we let G(r) denote the number of lattice points that lie inside and on the boundary of a given circle,
Gauss calculated that: G(1) = 5 G(2) = 13 G(3) = 29 G(4) = 49 G(5) = 81 G(6) = 113 G(7) = 149 . . . G(30) = 2821 . . . G(300) = 282,697,
Gauss cared because the function G(r) can be used to approximate 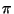 . i.e., . i.e.,
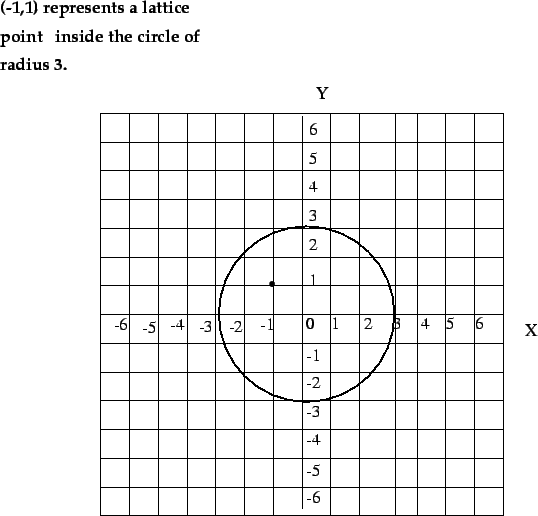
Figure 3 offers an illustration of circle of radius 3 with exactly 29 lattice points inside and on the boundary of the circle.
Figure:
circle of radius 3 with 29 lattice points
|
|
Other theorems that help us count the number of lattice points given by circles are the following:
theorem 1 (Steinhaus)
For every positive integer n, there exists a circle of area n which contains exactly n lattice points in its interior.
However this just tells us that such circles exist, but the following theorem describes how such circles can be found
explicitly.
theorem 2 (Schinzel's)
For every positive integer n, there is a circle in the plane having exactly n lattice points on its circumference. i.e.,
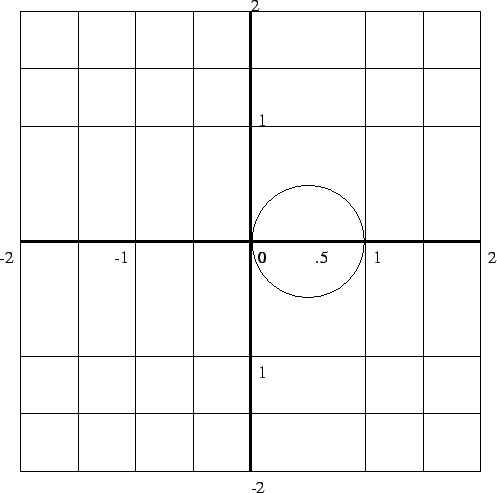
Consider the circle described by figure 4, in this case n is even, k = 1 radius is .5, and G(r) = 2.
Figure:
a case where n is even, k = 1, radius is .5
|
|
We have counted the number of lattice points that lie inside and on the boundary of a given circle. Suppose now we wanted to count the number of
lattice points of other curvy regions such as hyperbolas. For this, consider, the hyperbola
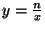 as illustrated in figure 5. Let
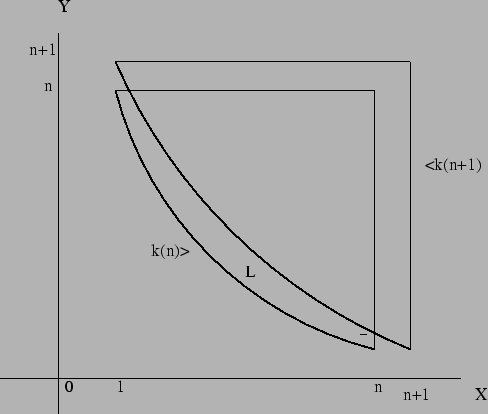
k(n) denote the number of lattice points given by the region k(n). Likewise, let k(n+1) be the number of lattice points given by the region
k(n+1). Moreover, let L be the strip as denoted in the figure. However, the boundary of L does not
include the boundary of k(n) nor of k(n+1). as illustrated in figure 5. Let
k(n) denote the number of lattice points given by the region k(n). Likewise, let k(n+1) be the number of lattice points given by the region
k(n+1). Moreover, let L be the strip as denoted in the figure. However, the boundary of L does not
include the boundary of k(n) nor of k(n+1).
Figure:
regions k(n) and k(n+1)
|
|
Given all of this, we arrive at the following theorem:
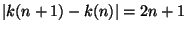 iff n is prime
Before proving observe that:
1) n is not prime
  (a,b) s.t. (a,b) = n (a,b) s.t. (a,b) = n
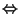 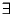 a lattice point (a,b) on
the lower boundary of k(n) s.t. (a,b) a lattice point (a,b) on
the lower boundary of k(n) s.t. (a,b) 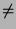 (n,1) or (1,n).
2) L has no lattice points (n,1) or (1,n).
2) L has no lattice points
 Proof: suppose n is not prime, then by observation one we have that Proof: suppose n is not prime, then by observation one we have that 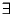 (a,b) s.t. ab = n, s.t. (a,b) (a,b) s.t. ab = n, s.t. (a,b)
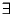 on the lower boundary of k(n) and (a,b)
on the lower boundary of k(n) and (a,b) 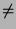 (n,1) or (1,n). Now suppose L has a lattice point (c,d) then (n,1) or (1,n). Now suppose L has a lattice point (c,d) then
However, this implies that n < cd < n+1 which is a contradiction since no integer can exist between
consecutive integers. Thus we have that given the premise n must be prime.
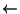 Now suppose n is prime then by observation one we have that n is prime
Now suppose n is prime then by observation one we have that n is prime
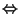 (n,1) and
(1,n) are lattice points. Also we have that region R does not have any lattice points. So if we count
we have n+1 lattice points on the upper boundary of region k(n+1) + n lattice points that exist on the
right hand side boundary of region k(n+1) + Q - [2 + Q] where Q denotes the intersection between regions k(n) and k(n+1).
After simplification we have that: (n,1) and
(1,n) are lattice points. Also we have that region R does not have any lattice points. So if we count
we have n+1 lattice points on the upper boundary of region k(n+1) + n lattice points that exist on the
right hand side boundary of region k(n+1) + Q - [2 + Q] where Q denotes the intersection between regions k(n) and k(n+1).
After simplification we have that:
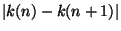 = 2n-1. qed.
|


![]() . Now, define a lattice point to be
an integer coordinate point lying on such a grid. Refer to figures 1 and 2 for examples of the above.
. Now, define a lattice point to be
an integer coordinate point lying on such a grid. Refer to figures 1 and 2 for examples of the above.
![]() as illustrated in figure 5. Let
k(n) denote the number of lattice points given by the region k(n). Likewise, let k(n+1) be the number of lattice points given by the region
k(n+1). Moreover, let L be the strip as denoted in the figure. However, the boundary of L does not
include the boundary of k(n) nor of k(n+1).
as illustrated in figure 5. Let
k(n) denote the number of lattice points given by the region k(n). Likewise, let k(n+1) be the number of lattice points given by the region
k(n+1). Moreover, let L be the strip as denoted in the figure. However, the boundary of L does not
include the boundary of k(n) nor of k(n+1).