Categorical diagonalization
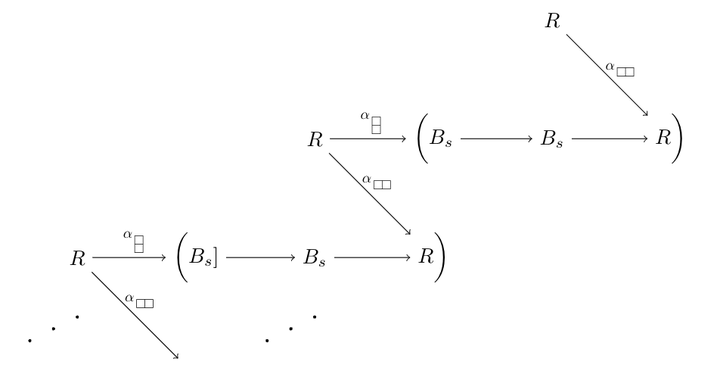 A twisted complex computing a categorified eigenspace projector.
A twisted complex computing a categorified eigenspace projector.
Abstract
This is an expository chapter in Springer’s “Introduction to Soergel Bimodules”. In classical linear algebra, given a diagonalizable operator on a vector space, Lagrange interpolation produces an idempotent decomposition of the identity corresponding to the projections to eigenspaces. In this chapter, we explain a categorical analogue of this procedure due to Elias and Hogancamp. Given a “diagonalizable” functor acting on a monoidal homotopy category, we produce idempotent functors which project to “eigencategories”. The main application is to the full twist Rouquier complex acting on the homotopy category of Soergel bimodules.
Type
Publication
In Springer