On the Strength of Chromatic Symmetric Homology for graphs
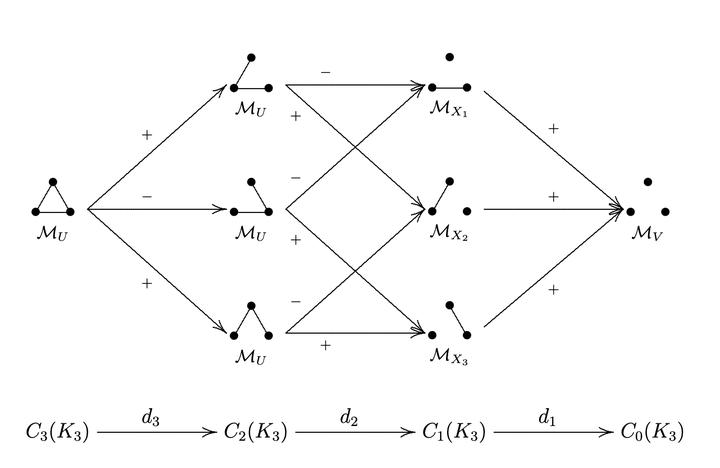 A diagram indicating how to compute chromatic symmetric homology for the triangle graph.
A diagram indicating how to compute chromatic symmetric homology for the triangle graph.
Abstract
In this paper, we investigate the strength of chromatic symmetric homology as a graph invariant. Chromatic symmetric homology is a lift of the chromatic symmetric function for graphs to a homological setting, and its Frobenius characteristic is a q,t generalization of the chromatic symmetric function. We exhibit three pairs of graphs where each pair has the same chromatic symmetric function but distinct homology. We also show that integral chromatic symmetric homology contains torsion and, based on computations, conjecture that torsion in bigrading (1,0) detects nonplanarity in the graph.
Type
Publication
On arXiv