Volume of a a parallelepiped

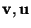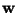Suppose three vectors ${\bf v } , {\bf u}$ and ${\bf w}$ in three dimensional space 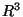$R^3$ are given so that they do not lie in the same plane. These three vectors form three edges of a parallelepiped. The volume of this parallelepiped ( is the product of area of the base and altitude ) is equal to the scalar triple product ${\bf u \cdot ( v \times w) }$ .

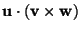It can be shown that the volume of the parallelepiped is the absolute value of the determinant of the following matrix:

$A=\left[ \begin{array}{rrr} u_1 & u_2 & u_3 \\ v_1 & v_2 & v_3 \\ w_1 & w_2 & w_3 \\ \end {array} \right]$.