Example 2

A common problem in this field is finding the probability of certain genotype after a given number of years. For example, suppose we want to study the fractions of the three genotypes in the $n^{th}$ generation of cows in terms of the initial genotype fractioins. (See the following example.)

Professor Vetar, at UC Davis, discovers that cows with genotype AA can produce a better quality milk than other genotypes. Professor Vetar is interested in discovering the fraction of offspring cows with genotype AA. If professor Vetar choses to cross only genotype $AA$ with other genotypes, what are the probabilities of the offspring being AA, Aa, or aa ?

To analyse the problem,we will consider three cases:

First assume, the crossing of AA with AA. This will always gives the genotype AA, therefore the probabilities of an offspring to be AA, Aa, and aa respectively are equal to 1, 0, and 0.

Second, assume crossing of Aa with AA. The offspring will have half chance to be of genotype AA and half chance the genotype Aa, therefore the probabilities of AA, Aa, and aa repectively are 1/2, 1/2, and 0.

Third, consider crossing of aa with AA. This will always results in genotype Aa. Therefore, the probabilities of genotypes AA, Aa, and aa repectively are 0, 1, and 0, respectively.

The following matrix is the result of the pervious obseration:

$$A = \left[ \begin{array}{rrr} 1&1/2&0\\ 0&1/2&1\\ 0&0&0\\ \end{array}\right]$$

This matrix can be veiwed as the following table:

$$\begin{array}{\vert c\vert c\vert c\vert c\vert} \hline {\m... ... 0 &AA \\ 0 &1/2 &1 &Aa \\ 0 &0 &0 &aa \\ \hline \end{array}$$

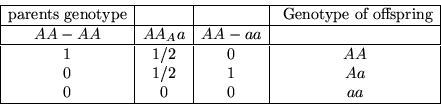
Assume that the initial prpulation of cows made up of an equal number of each genotype, therefore, the initial distribution vector $x_0$ is given by :

$$x_0= \left[ \begin{array}{r} 1/3\\ 1/3\\ 1/3\\ \end{array}\right]$$

One year later, the distribution is

$$x_1 = A x_0 = \left[ \begin{array}{c} \frac{ 1} {3} ( 1 + \fr... ... \left[ \begin{array}{r} 1/2\\ 1/2\\ 0\\ \end{array}\right]$$

After another year passed by, the distribution vector can be obtained as follow:

$x_2 = Ax_1 = A(A x_0 ) = A^2 x_0 = \left[ \begin{array}{r} 3/4\\ 1/4\\ 0\\ \end{array}\right].$

For any positive integer $n$, that is $n$ years later,

$$x_n = A^n x_0 = \left[ \begin{array}{r@{\qquad}r@{\qquad}r} ... ...\frac{1}{3}\\ \frac{1}{3}\\ \frac{1}{3}\\ \end{array}\right]$$

$$= \left[ \begin{array}{r@{\qquad}r@{\qquad}r} 1& \displaystyl... ...frac{1}{3}\\ \frac{1}{3}\\ \frac{1}{3}\\ \end{array}\right]$$

Now if $n$ gets larger and larger, the matrix $A^n$ approaches to

$$\left[ \begin{array}{rrr} 1&1&1\\ 0 & 0 & 0\\ 0 & 0 &0 \\ \end{array}\right]$$

Therefore $x_n = A^n x_0$ will approach to

$$\left[ \begin{array}{rrr} 1&1&1\\ 0 & 0 & 0\\ 0 & 0 & 0\\ ... ...t]= \left[ \begin{array}{r} 1\\ 0\\ 0\\ \end{array}\right]$$

Suppose someone is intested to see the number of cows with genotype AA, Aa, and aa after 20 geneations geneation. One way to answer this question is to compute $A^{20} x_0$ which may result in computaional error during the matrix multicaption. Another approach using of diagonalization reduces computation. If the matrix $A$ can be writen as product of an invertible matrix $P$ a diagonal matrix $D$ and inverse of $P$, that is $A = PD P^{-1}$, then computation wil be much simples and therefore much less comoutational error. This is mainly because of the following fact:

$$A^n = P D^n P^{-1}\hspace{2cm} \mbox{for } n = 1, 2, ...$$

and

$$D^n = \left[ \begin{array}{rrrrrrr} \lambda_1&0&0&.&.&.&0\\ ... ...&.& & & &.\\ 0&0&0&.&.&.&{\lambda_k}^{n}\\ \end{array}\right]$$

Not evey matrix $A$ is diagonalizable. For $A$ to be diagonalizable it needs to have $n$-linearly independent eigenvectors. The matrix $P$ is formed by writing these eigenvectors as columns of $P$. To find eigenvectors we will first find the eigenvalues.

For the matrix $A$ above the eigenvalues are

$$\lambda_1 = 1, \lambda_2 = 1/2, \lambda_3 = 0$$

and corresponding eigenvectors are:

$${\bf v_1 }= \left[ \begin{array}{r} 1\\ 0\\ 0\\ \end{array... ...3 }= \left[ \begin{array}{r} 1\\ -2\\ 1\\ \end{array}\right]$$

The diagonal matrix

$$D = \left[ \begin{array}{rrr} 1&0&0\\ 0&1/2&0\\ 0&0&0\\ \end{array}\right]$$

and

$$P = [ v_1\vert v_2\vert v_3 ] = \left[ \begin{array}{rrr} 1&1&1\\ 0&-1&-2\\ 0&0&1\\ \end{array}\right]$$

Therefore,

$x_n = P D^n P^{-1} x_0 \longrightarrow \left[ \begin{array}{r} 1\\ 0\\ 0\\ \end{array}\right]$ as n approach infinity..