An square matrix ![]() is called regular if for some integer
is called regular if for some integer ![]() all entries of
all entries of ![]() are positive.
are positive.
Example
The matrix
The matrix
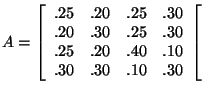
is a regular matrix, because ![]() has all positive entries.
has all positive entries.
It can also be shown that all other eigenvalues of A are less than 1, and algebraic multiplicity of 1 is one.
It can be shown that if ![]() is a regular matrix then
is a regular matrix then ![]() approaches to a matrix
approaches to a matrix ![]() whose columns are all equal to a probability vector
whose columns are all equal to a probability vector ![]() which is called the steady-state vector of the regular Markov chain.
which is called the steady-state vector of the regular Markov chain.
![\begin{displaymath}\mbox{ if } A \mbox{ regular, then } A^n \rightarrow Q = \lef...
...&&.\\
.&.&&&&.\\
q_k&q_k&.&.&.&q_k\\
\end{array}
\right]\end{displaymath}](img38.gif)
where
![]() .
.
It can be shown that for any probability vector ![]() when
when
![]() gets large,
gets large, ![]() approaches to the steady-state vector
approaches to the steady-state vector
![\begin{displaymath}{\bf q } = \left[ \begin{array}{r}
q_1\\
q_2\\
\vdots \\
q_k\\
\end{array}
\right]\end{displaymath}](img41.gif)
That is
![\begin{displaymath}A^n x^{(0)} \longrightarrow q=\left[ \begin{array}{r}
q_1\\
q_2\\
.\\
.\\
.\\
q_k\\
\end{array}
\right]\end{displaymath}](img42.gif)
where
![]() .
.
It can also be shown that the steady-state vector q is the only vector such that
Note that this shows q is an eigenvector of A and ![]() is eigenvalue of A.
is eigenvalue of A.