1. Enter matrices A and b by typing tex2html_wrap_inline15 and tex2html_wrap_inline17.

a) Show that Ax=b is inconsistent.( Hint: you may show this by finding tex2html_wrap_inline21 or finding both rank(A) and tex2html_wrap_inline25 )

b) You can enter tex2html_wrap_inline27 and A'*A by typing A'*A and A'* b in MATLAB. Show that the system tex2html_wrap_inline35 is a consistent system and find a solution for tex2html_wrap_inline37

c) Find the norm of the vector Ax-b by typing norm( Ax-b) where x is your solution from part (b).

i) Find a vector say , z, in column space of A by typing tex2html_wrap_inline47. compute || z -b|| by typing norm(z -b), compare this value with || Ax-b|| which one is smaller ?

ii) Find two other vectors, z, in cloumn space of A as we found z in part (i), find the norm of ||z -b|| for each of the points, z, and compare the results with || Ax-b||.

d) Is tex2html_wrap_inline27 invertible?

You may check this by

i) Finding tex2html_wrap_inline63 ( is it non-zero?) [Note : type det( A'* A)]

ii) Finding tex2html_wrap_inline67 ( Is it an identity matrix?)[Note : type rref( A'* A)]

e) Are the columns of A linearly independent?

f) Are the rows of A are linearly independent?

g) Find a basis for the column space of A.

h) Find a basis for the row space of A.

i) How many solutions does Ax=0 have?

j) What is the number of solutions of tex2html_wrap_inline81?

k) Find a basis for the range of the linear transformation tex2html_wrap_inline83? ( tex2html_wrap_inline83 is defined by T(x)= Ax)

l) Find a basis for the tex2html_wrap_inline89.

m) Find nullity of A , tex2html_wrap_inline83 and tex2html_wrap_inline27.

n) Find rank(A), tex2html_wrap_inline99, tex2html_wrap_inline101and tex2html_wrap_inline103.

2. Recall the following theorem: If A is an tex2html_wrap_inline105 matrix, then the following are equivalent:

i) Columns of A are linearly independent.

ii) tex2html_wrap_inline27 is an invertible matrix.

a) Determine if the following vectors are linearly independent.

tex2html_wrap_inline111

tex2html_wrap_inline113

tex2html_wrap_inline115

tex2html_wrap_inline117

(Note: form a matrix A whose columns are the vectors tex2html_wrap_inline119, then find tex2html_wrap_inline63.

b) Determine if the following vectors are linearly independent.

tex2html_wrap_inline123

tex2html_wrap_inline125

tex2html_wrap_inline127

3. Find an equation of the line that passes through the points ( 3,4) and (1,2).

a) Using the least square solution.

b) Using the regular way: finding slope and using slope intercept formula.

c) Did you get the same answer?

4. Consider the following set of points

(3, 4), (1,2), (-1, 1), (6,5), (7,9)

You may enter this points in a matrix by typing

tex2html_wrap_inline129

then X= D(:,1) is the matrix of x-values and Y=D(:,2) is the matrix of y-values.

i) Find a polynomial of degree two tex2html_wrap_inline135, that best fits the points given above.

Help

You need to form a tex2html_wrap_inline137 matrix A whose columns are square of the x values, x-values, and a column of ones. One way to do this is to type

tex2html_wrap_inline139

Note: Recall that the operations .* , .^ provide element wise multiplication and raising to a power.

Now in Ax=b the vector x is

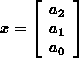
tex2html_wrap_inline145

and b is the vector of y-values. So you can enter b=D(:,2).

Now you could form the system AX=b, and least square solution id the solution of the normal system tex2html_wrap_inline151.

To solve this system you may find tex2html_wrap_inline153 by typing

tex2html_wrap_inline155

For the rest of this problem you need to redefine the matrix A > Make sure first clear yur old variables. For example for part (ii) first column of A is the third powers of x-value, and so on.



ii) Find a polynomial of degree three, tex2html_wrap_inline159 that best fits the points given above.



iii) Find a polynomial of degree four, tex2html_wrap_inline161 that best fits the points given above.



iv) Find a polynomial of degree five tex2html_wrap_inline163 that best fits the points given above.