Breaking polyhedra into pieces...
Tetrahedral Puzzles
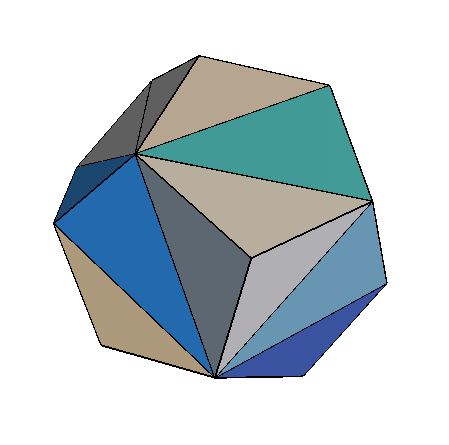
Do you feel like breaking things apart? May be this is the right place for you to express safely those feelings!! Here we look at decomposing or dissecting the solid volumes of convex polyhedra into tetrahedra. On the right picture we show one tetrahedral dissection of a dodecahedron.
But what is a dissection anyway? In our discussion we consider a finite collection of solid tetrahedra as the pieces of a three dimensional puzzle that must fully cover the interior of the polyhedron being partitioned. We further assume that any two tetrahedra have disjoint interior. If in addition we have that the intersection of any pair of tetrahedra is either empty or a common point, edge or triangular face we have a triangulation.
For the curious reader, I explained, via examples, two general questions I like that have to do with dissections and triangulations:
Cut out printouts of unfolded tetrahedra. The challenge is to build a regular cube in at least two different ways using the pieces. Can you do it in three different ways? You can also look at the answers. How many triangulations are possible of regular cube? Counting how many triangulations are possible is a hard problem.
Suppose you are given a regular icosahedron instead of a cube. What is the smallest (maximal) number of tetrahedra in a dissection? Why? Look here for the answers and some more models. You can also look at the solution of the same questions for the dodecahedron, included a short movie. Finding optimal subdivisions is a problem with connections to topology and algebraic geometry.