Benjamin Makoto Godkin
CV

I am a sixth year student of the Graduate Group in Applied Mathematics interested in partial differential equations and numerical analysis, and my advisor is Joseph Teran. Watching smoke billow from campfires and the cyles of boiling and boiling over wort, my inspiration for studying applied mathematics stems from the uncanny ability of using mathematics to model various physical phonomena.
Before coming to Davis in the fall of 2019, I earned a BS in Applied Mathematics at UCLA in 2015, worked a couple of years in legal tech at Ravel Law, and completed an MS in Mathematics at San José State University. While at San José State, I researched finite element methods for Burgers' equation, and my advisor was Daniel Brinkman. Below is an application of the Discontinuous Galerkin Method to the inviscid Burgers' equation.
Classes for which I was a teaching assistant:
Winter 2025 - MAT 21C (Teran)
Spring 2024 - MAT 128B (Islambouli)
Winter 2024 - MAT 21C (Teran)
Fall 2023 - MAT 17A (Dad-del)
Fall 2023 - MAT 17A (Alameda)
Spring 2023 - MAT 128B (Schonsheck)
Winter 2023 - MAT 21C (Thompson)
Fall 2022 - MAT 128A (Grønbech-Jensen)
Fall 2022 - MAT 228A (Guy)
Spring 2022 - MAT 17C (Saito)
Winter 2022 - MAT 17B (De Loera)
Fall 2021 - MAT 17A (Guy)
Spring 2021 - MAT 17C (Lewis)
Winter 2021 - MAT 21C (Waldron)
Fall 2020 - MAT 17A (Guy)
Spring 2020 - MAT 17C (Rademacher)
Winter 2020 - MAT 21C (Temple)
Fall 2019 - MAT 17A (Dad-del)
Classes for which I was the instructor of record:
Spring 2025 - MAT 22A
Summer Session II 2024 - MAT 128A
Summer Session I 2023 - MAT 22B
Summer Session II 2022 - MAT 22B
Summer Session I 2022 - MAT 22B
Summer Session I 2021 - MAT 22B
Summer Session I 2020 - MAT 22A
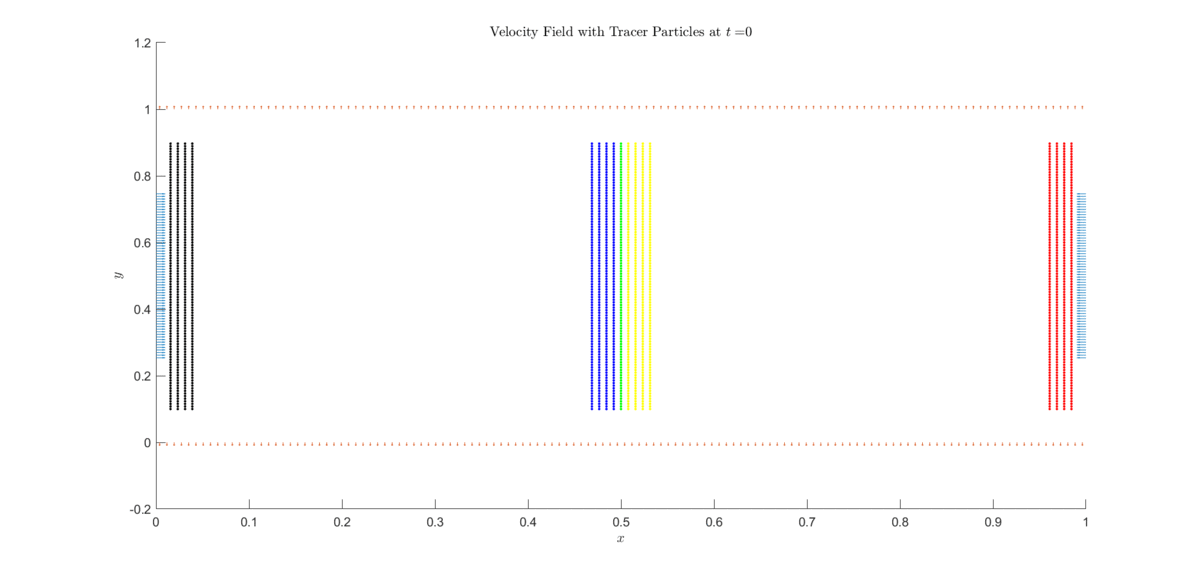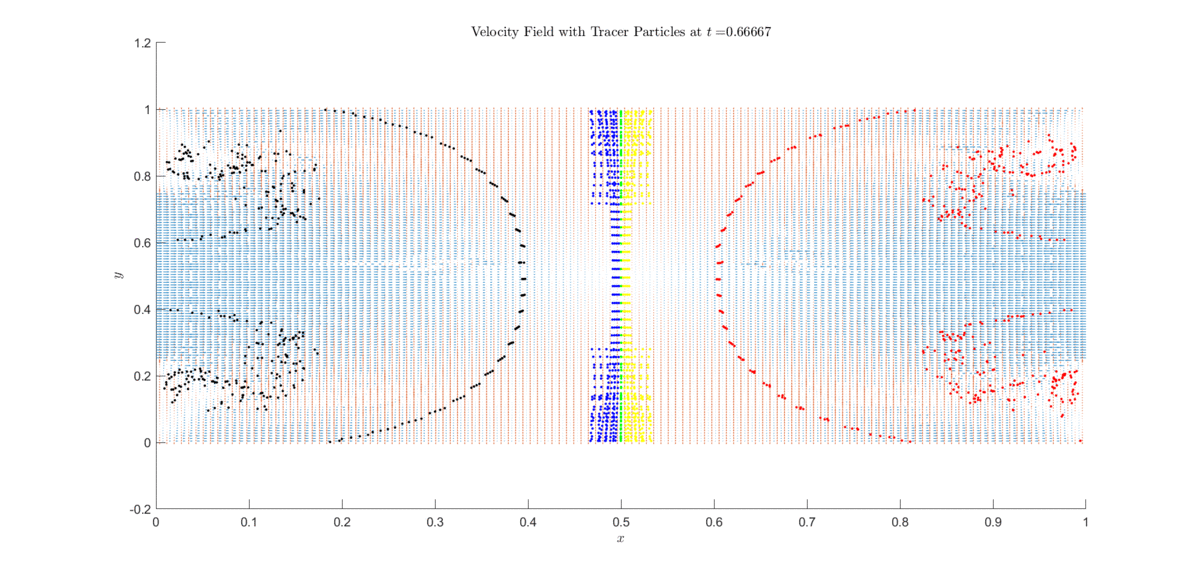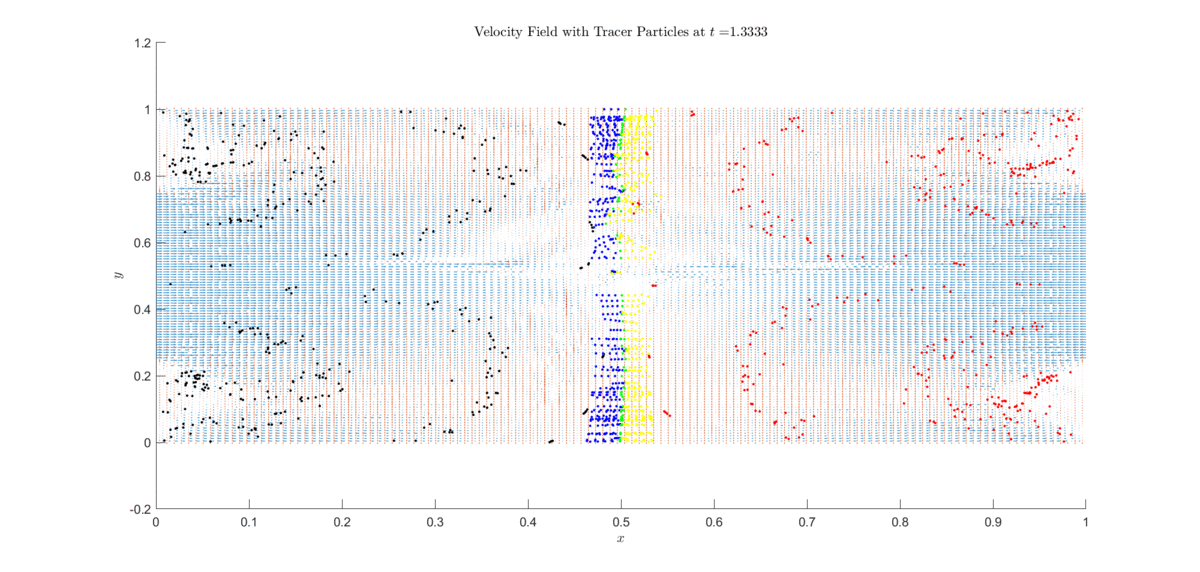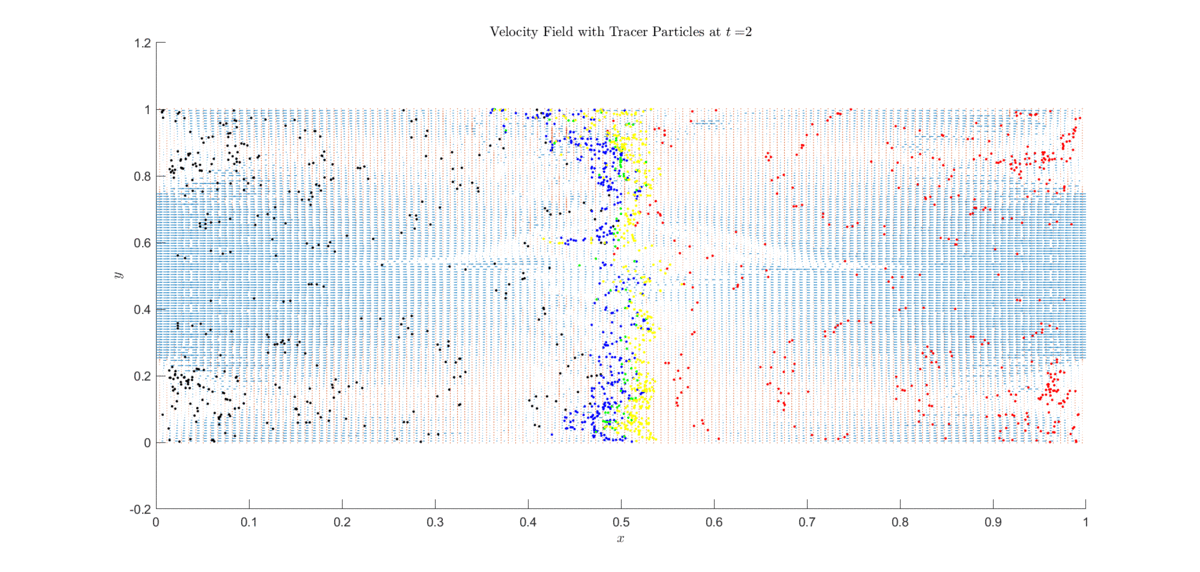
Below is an application of an explicit semi-Lagrangian scheme approximating the incompressible Euler equations.