![]() .
.
However, we rarely use this formal approach when applying the chain rule to specific problems. Instead, we invoke an intuitive approach. For example, it is sometimes easier to think of the functions f and g as ``layers'' of a problem. Function f is the ``outer layer'' and function g is the ``inner layer.'' Thus, the chain rule tells us to first differentiate the outer layer, leaving the inner layer unchanged (the term f'( g(x) ) ) , then differentiate the inner layer (the term g'(x) ) . This process will become clearer as you do the problems. In most cases, final answers are given in the most simplified form.
Click HERE to see a detailed solution to problem 1.
Click HERE to see a detailed solution to problem 2.
Click HERE to see a detailed solution to problem 3.
Click HERE to see a detailed solution to problem 4.
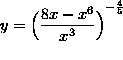 .
.
Click HERE to see a detailed solution to problem 5.
Click HERE to see a detailed solution to problem 6.
Click HERE to see a detailed solution to problem 7.
Click HERE to see a detailed solution to problem 8.
Click HERE to see a detailed solution to problem 9.
Click HERE to see a detailed solution to problem 10.
Click HERE to see a detailed solution to problem 11.
Click HERE to see a detailed solution to problem 12.
Click HERE to see a detailed solution to problem 13.
Click HERE to see a detailed solution to problem 14.
Click HERE to see a detailed solution to problem 15.
Click HERE to see a detailed solution to problem 16.
Click HERE to see a detailed solution to problem 17.
Click HERE to see a detailed solution to problem 18.
Click HERE to see a detailed solution to problem 19.
Click HERE to see a detailed solution to problem 20.
Click HERE to see a detailed solution to problem 21.
Your comments and suggestions are welcome. Please e-mail any correspondence to Duane Kouba by clicking on the following address :