( The outer layer is ``the square'' and the inner layer is (3x+1) . Differentiate ``the square'' first, leaving (3x+1) unchanged. Then differentiate (3x+1). ) Thus,
![]()
= 2 (3x+1) (3)
= 6 (3x+1) .
Click HERE to return to the list of problems.
SOLUTION 2 : Differentiate ![]() .
.
( The outer layer is ``the square root'' and the inner layer is ![]() . Differentiate ``the square root'' first, leaving
. Differentiate ``the square root'' first, leaving ![]() unchanged. Then differentiate
unchanged. Then differentiate ![]() . ) Thus,
. ) Thus,
![]()
![]()
![]()
![]()
![]()
Click HERE to return to the list of problems.
SOLUTION 3 : Differentiate ![]() .
.
( The outer layer is ``the 30th power'' and the inner layer is ![]() . Differentiate ``the 30th power'' first, leaving
. Differentiate ``the 30th power'' first, leaving ![]() unchanged. Then differentiate
unchanged. Then differentiate ![]() . ) Thus,
. ) Thus,
![]()
![]()
![]()
Click HERE to return to the list of problems.
SOLUTION 4 : Differentiate ![]() .
.
( The outer layer is ``the one-third power'' and the inner layer is ![]() . Differentiate ``the one-third power'' first, leaving
. Differentiate ``the one-third power'' first, leaving ![]() unchanged. Then differentiate
unchanged. Then differentiate ![]() . ) Thus,
. ) Thus,
![]()
![]()
(At this point, we will continue to simplify the expression, leaving the final answer with no negative exponents.)
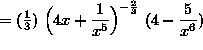
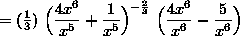
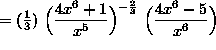
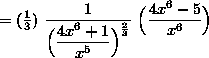
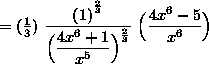
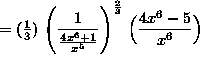
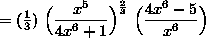
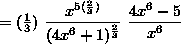
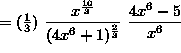
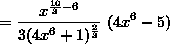
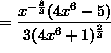
![]() .
.
Click HERE to return to the list of problems.
SOLUTION 5 : Differentiate 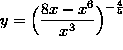 .
.
( First, begin by simplifying the expression before we differentiate it. ) Thus,
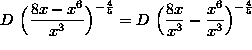
![]()
( The outer layer is ``the negative four-fifths power'' and the inner layer is ![]() . Differentiate ``the negative four-fifths power'' first, leaving
. Differentiate ``the negative four-fifths power'' first, leaving ![]() unchanged. Then differentiate
unchanged. Then differentiate ![]() . )
. )
![]()
![]()
(At this point, we will continue to simplify the expression, leaving the final answer with no negative exponents.)
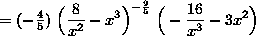
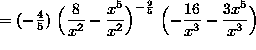
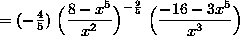
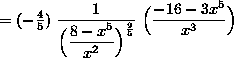
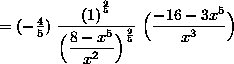
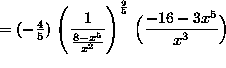
![]()
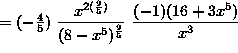
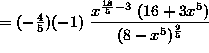
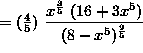
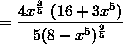 .
.
Click HERE to return to the list of problems.
SOLUTION 6 : Differentiate ![]() .
.
( The outer layer is ``the sine function'' and the inner layer is (5x) . Differentiate ``the sine function'' first, leaving (5x) unchanged. Then differentiate (5x) . ) Thus,
![]()
![]()
![]() .
.
Click HERE to return to the list of problems.
SOLUTION 7 : Differentiate ![]() .
.
( The outer layer is ``the exponential function'' and the inner layer is ![]() . Recall that
. Recall that
![]() . Differentiate ``the exponential function'' first, leaving
. Differentiate ``the exponential function'' first, leaving ![]() unchanged. Then differentiate
unchanged. Then differentiate ![]() . ) Thus,
. ) Thus,
![]()
![]()
![]() .
.
Click HERE to return to the list of problems.
SOLUTION 8 : Differentiate ![]() .
.
( The outer layer is ``2 raised to a power'' and the inner layer is ![]() . Recall that
. Recall that
![]() . Differentiate ``2 raised to a power'' first, leaving
. Differentiate ``2 raised to a power'' first, leaving ![]() unchanged. Then differentiate
unchanged. Then differentiate ![]() . ) Thus,
. ) Thus,
![]()
![]()
![]() .
.
Click HERE to return to the list of problems.
SOLUTION 9 : Differentiate ![]() .
.
( Since 3 is a MULTIPLIED CONSTANT, we will first use the rule ![]() , where c is a constant . Hence, the constant 3 just ``tags along'' during the differentiation process. It is NOT necessary to use the product rule. ) Thus,
, where c is a constant . Hence, the constant 3 just ``tags along'' during the differentiation process. It is NOT necessary to use the product rule. ) Thus,
![]()
( Now the outer layer is ``the tangent function'' and the inner layer is ![]() . Differentiate ``the tangent function'' first, leaving
. Differentiate ``the tangent function'' first, leaving ![]() unchanged. Then differentiate
unchanged. Then differentiate ![]() . )
. )
![]()
![]()
![]()
![]()
![]() .
.
Click HERE to return to the list of problems.
SOLUTION 10 : Differentiate ![]() .
.
( The outer layer is ``the natural logarithm (base e) function'' and the inner layer is ( 17-x ) . Recall that ![]() . Differentiate ``the natural logarithm function'' first, leaving ( 17-x ) unchanged. Then differentiate ( 17-x ). ) Thus,
. Differentiate ``the natural logarithm function'' first, leaving ( 17-x ) unchanged. Then differentiate ( 17-x ). ) Thus,
![]()
![]()
![]() .
.
Click HERE to return to the list of problems.
SOLUTION 11 : Differentiate ![]() .
.
( The outer layer is ``the common logarithm (base 10) function'' and the inner layer is ![]() . Recall that
. Recall that ![]() . Differentiate ``the common logarithm (base 10) function'' first, leaving
. Differentiate ``the common logarithm (base 10) function'' first, leaving ![]() unchanged. Then differentiate
unchanged. Then differentiate ![]() . ) Thus,
. ) Thus,
![]()
![]()
![]() .
.
Click HERE to return to the list of problems.
( Recall that ![]() , which makes ``the square'' the outer layer, NOT ``the cosine function''. In fact, this problem has three layers. The first layer is ``the square'', the second layer is ``the cosine function'', and the third layer is
, which makes ``the square'' the outer layer, NOT ``the cosine function''. In fact, this problem has three layers. The first layer is ``the square'', the second layer is ``the cosine function'', and the third layer is ![]() . Differentiate ``the square'' first, leaving ``the cosine function'' and
. Differentiate ``the square'' first, leaving ``the cosine function'' and ![]() unchanged. Then differentiate ``the cosine function'', leaving
unchanged. Then differentiate ``the cosine function'', leaving ![]() unchanged. Finish with the derivative of
unchanged. Finish with the derivative of ![]() . ) Thus,
. ) Thus,
![]()
![]()
![]()
![]()
![]() .
.
Click HERE to return to the list of problems.
SOLUTION 13 : Differentiate ![]() .
.
( Since ![]() is a MULTIPLIED CONSTANT, we will first use the rule
is a MULTIPLIED CONSTANT, we will first use the rule ![]() , where c is a constant. Hence, the constant
, where c is a constant. Hence, the constant ![]() just ``tags along'' during the differentiation process. It is NOT necessary to use the product rule. ) Thus,
just ``tags along'' during the differentiation process. It is NOT necessary to use the product rule. ) Thus,
![]()
( Recall that ![]() , which makes ``the negative four power'' the outer layer, NOT ``the secant function''. In fact, this problem has three layers. The first layer is ``the negative four power'', the second layer is ``the secant function'', and the third layer is
, which makes ``the negative four power'' the outer layer, NOT ``the secant function''. In fact, this problem has three layers. The first layer is ``the negative four power'', the second layer is ``the secant function'', and the third layer is ![]() . Differentiate ``the negative four power'' first, leaving ``the secant function'' and
. Differentiate ``the negative four power'' first, leaving ``the secant function'' and ![]() unchanged. Then differentiate ``the secant function'', leaving
unchanged. Then differentiate ``the secant function'', leaving ![]() unchanged. Finish with the derivative of
unchanged. Finish with the derivative of ![]() . )
. )
![]()
![]()
![]()
![]()
![]() .
.
Click HERE to return to the list of problems.
SOLUTION 14 : Differentiate ![]() .
.
( There are four layers in this problem. The first layer is ``the natural logarithm (base e) function'', the second layer is ``the fifth power'', the third layer is ``the cosine function'', and the fourth layer is ![]() . Differentiate them in that order. ) Thus,
. Differentiate them in that order. ) Thus,
![]()
![]()
![]()
![]()
![]()
![]()
![]() .
.
Click HERE to return to the list of problems.
SOLUTION 15 : Differentiate ![]() .
.
( There are four layers in this problem. The first layer is ``the square root function'', the second layer is ``the sine function'', the third layer is `` 7x plus the natural logarithm (base e) function'', and the fourth layer is (5x) . Differentiate them in that order. ) Thus,
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]() .
.
Click HERE to return to the list of problems.
SOLUTION 16 : Differentiate ![]() .
.
( Since 10 is a MULTIPLIED CONSTANT, we will first use the rule ![]() , where c is a constant. Hence, the constant 10 just ``tags along'' during the differentiation process. It is NOT necessary to use the product rule. ) Thus,
, where c is a constant. Hence, the constant 10 just ``tags along'' during the differentiation process. It is NOT necessary to use the product rule. ) Thus,
![]()
( Now there are four layers in this problem. The first layer is ``the fifth power'', the second layer is ``1 plus the third power '', the third layer is ``2 minus the ninth power'', and the fourth layer is ![]() . Differentiate them in that order. )
. Differentiate them in that order. )
![]()
![]()
![]()
![]()
![]() .
.
Click HERE to return to the list of problems.
SOLUTION 17 : Differentiate ![]() .
.
( Since 4 is a MULTIPLIED CONSTANT, we will first use the rule ![]() , where c is a constant. Hence, the constant 4 just ``tags along'' during the differentiation process. It is NOT necessary to use the product rule. ) Thus,
, where c is a constant. Hence, the constant 4 just ``tags along'' during the differentiation process. It is NOT necessary to use the product rule. ) Thus,
![]()
( There are four layers in this problem. The first layer is ``the natural logarithm (base e) function'', the second layer is ``the natural logarithm (base e) function'', the third layer is ``the natural logarithm (base e) function'', and the fourth layer is ![]() . Differentiate them in that order. )
. Differentiate them in that order. )
![]()
![]()
![]()
![]()
![]() .
.
Click HERE to return to the list of problems.
SOLUTION 18 : Differentiate ![]() .
.
( There are four layers in this problem. The first layer is ``the third power'', the second layer is ``the tangent function'', the third layer is ``the square root function'', the fourth layer is ``the cotangent function'', and the fifth layer is (7x) . Differentiate them in that order. ) Thus,
![]()
![]()
![]()
![]()
![]()
![]()
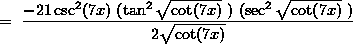 .
.
The following three problems require a more formal use of the chain rule.
Click HERE to return to the list of problems.
SOLUTION 19 : Assume that h(x) = f( g(x) ) , where both f and g are differentiable functions. If g(-1)=2, g'(-1)=3, and f'(2)=-4 , what is the value of h'(-1) ?
Recall that the chain rule states that ![]() . Thus,
. Thus,
![]()
so that
![]() .
.
Click HERE to return to the list of problems.
SOLUTION 20 : Assume that ![]() , where f is a differentiable function. If
, where f is a differentiable function. If ![]() and
and ![]() , determine an equation of the line tangent to the graph of h at x=0 .
, determine an equation of the line tangent to the graph of h at x=0 .
The outer layer of this function is ``the third power'' and the inner layer is f(x) . The chain rule gives us that the derivative of h is
![]() .
.
Thus, the slope of the line tangent to the graph of h at x=0 is
![]() .
.
This line passes through the point ![]() . Using the point-slope form of a line, an equation of this tangent line is
. Using the point-slope form of a line, an equation of this tangent line is
![]() or
or ![]() .
.
Click HERE to return to the list of problems.
SOLUTION 21 : Determine a differentiable function y = f(x) which has the properties
![]() and
and ![]() .
.
Begin with ![]() and assume that f(x) is not identically zero. Then
and assume that f(x) is not identically zero. Then
![]() iff
iff ![]() .
.
Note that
![]()
and
![]() , where C is any constant .
, where C is any constant .
Now think about ``reversing'' the process of differentiation. This is called finding an antiderivative. Thus,
![]() iff
iff
![]()
iff ![]() .
.
Since ![]() , we have
, we have ![]() so that
so that
![]() and C = 2 . Thus,
and C = 2 . Thus,
![]() .
.
Click HERE to return to the list of problems.