The following problems involve the CONTINUITY OF A FUNCTION OF ONE VARIABLE. Function y = f(x) is continuous at point x=a if the following three conditions are satisfied :
i.) f(a) is defined ,
ii.)
![]() exists (i.e., is finite) ,
exists (i.e., is finite) ,
and
iii.)
![]() .
.
Function f is said to be continuous on an interval I if f is continuous at each point x in I. Here is a list of some well-known facts related to continuity :
1. The SUM of continuous functions is continuous.
2. The DIFFERENCE of continuous functions is continuous.
3. The PRODUCT of continuous functions is continuous.
4. The QUOTIENT of continuous functions is continuous at all points x where the DENOMINATOR IS NOT ZERO.
5. The FUNCTIONAL COMPOSITION of continuous functions is continuous at all points x where the composition is properly defined.
6. Any polynomial is continuous for all values of x.
7. Function ex and trigonometry functions ![]() and
and ![]() are continuous for all values of x.
are continuous for all values of x.
Most problems that follow are average. A few are somewhat challenging. All limits are determined WITHOUT the use of
L'Hopital's Rule. If you are going to try these problems before looking at the solutions, you can avoid common
mistakes by using the above step-by-step definition of continuity at a point and the well-known facts, and by giving careful consideration to the indeterminate form
![]() during the computation of limits. Knowledge of one-sided limits will be required. For a review of limits and indeterminate forms click here.
during the computation of limits. Knowledge of one-sided limits will be required. For a review of limits and indeterminate forms click here.
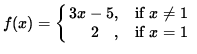
Click HERE to see a detailed solution to problem 1.
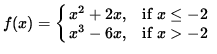
Click HERE to see a detailed solution to problem 2.
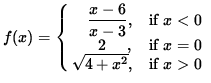
Click HERE to see a detailed solution to problem 3.
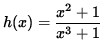 is continuous at x=-1 .
is continuous at x=-1 .
Click HERE to see a detailed solution to problem 4.
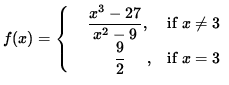
Click HERE to see a detailed solution to problem 5.
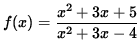 continuous ?
continuous ?
Click HERE to see a detailed solution to problem 6.
Click HERE to see a detailed solution to problem 7.
Click HERE to see a detailed solution to problem 8.
Click HERE to see a detailed solution to problem 9.
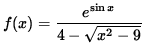 continuous ?
continuous ?
Click HERE to see a detailed solution to problem 10.
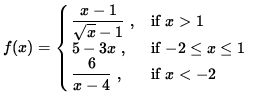
Click HERE to see a detailed solution to problem 11.
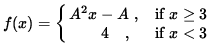
Click HERE to see a detailed solution to problem 12.
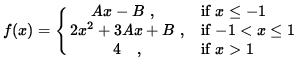
Click HERE to see a detailed solution to problem 13.
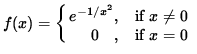
Click HERE to see a detailed solution to problem 14.
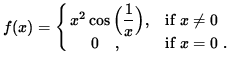
Show that f is continuous for all values of x . Show that f is differentiable for all values of x, but that the derivative, f' , is NOT CONTINUOUS at x=0 .
Click HERE to see a detailed solution to problem 15.
Your comments and suggestions are welcome. Please e-mail any correspondence to Duane Kouba by clicking on the following address :