SOLUTION 1 : Function f is defined at x=1 since
i.) f(1) = 2 .
The limit
![]()
= 3 (1) - 5
= -2 ,
i.e.,
ii.)
![]() .
.
But
iii.)
![]() ,
,
so condition iii.) is not satisfied and function f is NOT continuous at x=1 .
Click HERE to return to the list of problems.
SOLUTION 2 : Function f is defined at x=-2 since
i.) f(-2) = (-2)2 + 2(-2) = 4-4 = 0 .
The left-hand limit
![]()
= (-2)2 + 2(-2)
= 4 - 4
= 0 .
The right-hand limit
![]()
= (-2)3 - 6(-2)
= -8 + 12
= 4 .
Since the left- and right-hand limits are not equal, ,
ii.)
![]() does not exist,
does not exist,
and condition ii.) is not satisfied. Thus, function f is NOT continuous at x=-2 .
Click HERE to return to the list of problems.
SOLUTION 3 : Function f is defined at x=0 since
i.) f(0) = 2 .
The left-hand limit
![]()
![]()
= 2 .
The right-hand limit
![]()
![]()
![]()
= 2 .
Thus,
![]() exists with
exists with
ii.)
![]() .
.
Since
iii.)
![]() ,
,
all three conditions are satisfied, and f is continuous at x=0 .
Click HERE to return to the list of problems.
SOLUTION 4 : Function h is not defined at x=-1 since it leads to division by zero. Thus,
i.) h(-1)
does not exist, condition i.) is violated, and function h is NOT continuous at x = -1 .
Click HERE to return to the list of problems.
SOLUTION 5 : First, check for continuity at x=3 . Function f is defined at x=3 since
i.)
![]() .
.
The limit
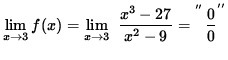
(Circumvent this indeterminate form by factoring the numerator and the denominator.)
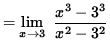
(Recall that A2 - B2 = (A-B)(A+B) and A3 - B3 = (A-B)(A2+AB+B2 ) . )
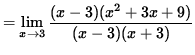
(Divide out a factor of (x-3) . )
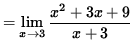
=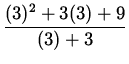
![]()
![]() ,
,
i.e.,
ii.)
![]() .
.
Since,
iii.)
![]() ,
,
all three conditions are satisfied, and f is continuous at x=3 . Now, check for continuity at x=-3 . Function f is not defined at x = -3 because of division by zero. Thus,
i.) f(-3)
does not exist, condition i.) is violated, and f is NOT continuous at x=-3 .
Click HERE to return to the list of problems.
SOLUTION 6 : Functions
y = x2 + 3x + 5 and
y = x2 + 3x - 4 are continuous for all values of x since both are polynomials. Thus, the quotient of these two functions,
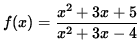 ,
is continuous for all values of x where the denominator,
y = x2 + 3x - 4 = (x-1)(x+4) , does NOT equal zero. Since
(x-1)(x+4) = 0 for x=1 and x=-4 , function f is continuous for all values of x EXCEPT x=1 and x=-4 .
,
is continuous for all values of x where the denominator,
y = x2 + 3x - 4 = (x-1)(x+4) , does NOT equal zero. Since
(x-1)(x+4) = 0 for x=1 and x=-4 , function f is continuous for all values of x EXCEPT x=1 and x=-4 .
Click HERE to return to the list of problems.
SOLUTION 7 : First describe function g using functional composition. Let
f(x) = x1/3 ,
![]() , and
k(x) = x20 + 5 . Function k is continuous for all values of x since it is a polynomial, and functions f and h are well-known to be continuous for all values of x . Thus, the functional compositions
, and
k(x) = x20 + 5 . Function k is continuous for all values of x since it is a polynomial, and functions f and h are well-known to be continuous for all values of x . Thus, the functional compositions
![]()
and
![]()
are continuous for all values of x . Since
![]() ,
,
function g is continuous for all values of x .
Click HERE to return to the list of problems.
SOLUTION 8 : First describe function f using functional composition. Let
g(x) = x2 - 2x and
![]() . Function g is continuous for all values of x since it is a polynomial, and function h is well-known to be continuous for
. Function g is continuous for all values of x since it is a polynomial, and function h is well-known to be continuous for ![]() . Since
g(x) = x2 - 2x = x(x-2) , it follows easily that
. Since
g(x) = x2 - 2x = x(x-2) , it follows easily that
![]() for
for ![]() and
and ![]() . Thus, the functional composition
. Thus, the functional composition
![]()
is continuous for ![]() and
and ![]() . Since
. Since
![]() ,
,
function f is continuous for ![]() and
and ![]() .
.
Click HERE to return to the list of problems.
SOLUTION 9 : First describe function f using functional composition.
Let
![]() and
and
![]() . Since g is the quotient of polynomials
y = x-1 and y = x+2 , function g is continuous for all values of x EXCEPT where x+2 = 0 , i.e., EXCEPT for x = -2 . Function h is well-known to be continuous for x > 0 . Since
. Since g is the quotient of polynomials
y = x-1 and y = x+2 , function g is continuous for all values of x EXCEPT where x+2 = 0 , i.e., EXCEPT for x = -2 . Function h is well-known to be continuous for x > 0 . Since
![]() , it follows easily that g(x) > 0 for x < -2 and x > 1 . Thus, the functional composition
, it follows easily that g(x) > 0 for x < -2 and x > 1 . Thus, the functional composition
![]()
is continuous for x < -2 and x > 1 . Since
![]() ,
,
function f is continuous for x < -2 and x > 1 .
Click HERE to return to the list of problems.
SOLUTION 10 : First describe function f using functional composition.
Let
![]() and
h(x) = e x , both of which are well-known to be continuous for all values of x . Thus, the numerator
and
h(x) = e x , both of which are well-known to be continuous for all values of x . Thus, the numerator
![]() is continuous (the functional composition of continuous functions) for all values of x . Now consider the denominator
is continuous (the functional composition of continuous functions) for all values of x . Now consider the denominator
![]() . Let g(x) = 4 ,
h(x) = x2 - 9 , and
. Let g(x) = 4 ,
h(x) = x2 - 9 , and
![]() . Functions g and h are continuous for all values of x since both are polynomials, and it is well-known that function k is continuous for
. Functions g and h are continuous for all values of x since both are polynomials, and it is well-known that function k is continuous for ![]() . Since
h(x) = x2 - 9 = (x-3)(x+3) = 0 when x=3 or x=-3 , it follows easily that
. Since
h(x) = x2 - 9 = (x-3)(x+3) = 0 when x=3 or x=-3 , it follows easily that
![]() for
for ![]() and
and ![]() , so that
, so that
![]() is continuous (the functional composition of continuous functions) for
is continuous (the functional composition of continuous functions) for ![]() and
and ![]() . Thus, the denominator
. Thus, the denominator
![]() is continuous (the difference of continuous functions) for
is continuous (the difference of continuous functions) for ![]() and
and ![]() . There is one other important consideration. We must insure that the DENOMINATOR IS NEVER ZERO. If
. There is one other important consideration. We must insure that the DENOMINATOR IS NEVER ZERO. If
![]()
then
![]() .
.
Squaring both sides, we get
16 = x2 - 9
so that
x2 = 25
when
x = 5 or x = -5 .
Thus, the denominator is zero if x = 5 or x = -5 . Summarizing, the quotient of these continuous functions,
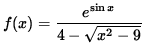 , is continuous for
, is continuous for ![]() and
and ![]() , but NOT for x = 5 and x = -5 .
, but NOT for x = 5 and x = -5 .
Click HERE to return to the list of problems.
SOLUTION 11 : Consider separately the three component functions which determine f . Function
![]() is continuous for x > 1 since it is the quotient of continuous functions and the denominator is never zero. Function y = 5 -3x is continuous for
is continuous for x > 1 since it is the quotient of continuous functions and the denominator is never zero. Function y = 5 -3x is continuous for
![]() since it is a polynomial. Function
since it is a polynomial. Function
![]() is continuous for x < -2 since it is the quotient of continuous functions and the denominator is never zero. Now check for continuity of f where the three components are joined together, i.e., check for continuity at x=1 and x=-2 . For x = 1 function f is defined since
is continuous for x < -2 since it is the quotient of continuous functions and the denominator is never zero. Now check for continuity of f where the three components are joined together, i.e., check for continuity at x=1 and x=-2 . For x = 1 function f is defined since
i.) f(1) = 5 - 3(1) = 2 .
The right-hand limit
![]() =
=
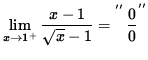
(Circumvent this indeterminate form one of two ways. Either factor the numerator as the difference of squares, or multiply by the conjugate of the denominator over itself.)
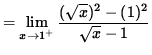
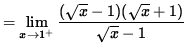
![]()
![]()
= 2 .
The left-hand limit
![]() =
=
![]()
= 5 - 3(1)
= 2 .
Thus,
ii.)
![]() .
.
Since
iii.)
![]() ,
,
all three conditions are satisfied, and function f is continuous at x=1 . Now check for continuity at x=-2 . Function f is defined at x=-2 since
i.) f(-2) = 5 - 3(-2) = 11 .
The right-hand limit
![]() =
=
![]()
= 5 - 3( -2)
= 11 .
The left-hand limit
![]() =
=
![]()
![]()
![]()
= -1 .
Since the left- and right-hand limits are different,
ii.)
![]() does NOT exist,
does NOT exist,
condition ii.) is violated, and function f is NOT continuous at x=-2 . Summarizing, function f is continuous for all values of x EXCEPT x=-2 .
Click HERE to return to the list of problems.
SOLUTION 12 : First, consider separately the two components which determine function f . Function
y = A2 x - A is continuous for ![]() for any value of A since it is a polynomial. Function y = 4 is continuous for x < 3 since it is a polynomial. Now determine A so that function f is continuous at x=3 . Function f must be defined at x=3 , so
for any value of A since it is a polynomial. Function y = 4 is continuous for x < 3 since it is a polynomial. Now determine A so that function f is continuous at x=3 . Function f must be defined at x=3 , so
i.) f(3)= A2 (3) - A = 3 A2 - A .
The right-hand limit
![]() =
=
![]()
= A2 (3) - A
= 3 A2 - A .
The left-hand limit
![]() =
=
![]()
= 4 .
For the limit to exist, the right- and left-hand limits must exist and be equal. Thus,
ii.)
![]() ,
,
so that
3 A2 - A - 4 = 0 .
Factoring, we get
(3A - 4)(A + 1) = 0
for
![]() or A = -1 .
or A = -1 .
For either choice of A ,
iii.)
![]() ,
,
all three conditions are satisfied, and f is continuous at x=3 . Therefore, function f is continuous for all values of x if
![]() or A = -1 .
or A = -1 .
Click HERE to return to the list of problems.
SOLUTION 13 : First, consider separately the three components which determine function f . Function
y = Ax - B is continuous for ![]() for any values of A and B since it is a polynomial. Function
y = 2x2 + 3Ax + B is continuous for
for any values of A and B since it is a polynomial. Function
y = 2x2 + 3Ax + B is continuous for
![]() for any values of A and B since it is a polynomial. Function y = 4 is continuous for x > 1 since it is a polynomial. Now determine A and B so that function f is continuous at x=-1 and x=1 . First, consider continuity at x=-1 . Function f must be defined at x=-1 , so
for any values of A and B since it is a polynomial. Function y = 4 is continuous for x > 1 since it is a polynomial. Now determine A and B so that function f is continuous at x=-1 and x=1 . First, consider continuity at x=-1 . Function f must be defined at x=-1 , so
i.) f(-1)= A(-1) - B = - A - B .
The left-hand limit
![]() =
=
![]()
= A (-1) - B
= - A - B .
The right-hand limit
![]() =
=
![]()
= 2(-1)2 + 3A(-1) + B
= 2 - 3A + B .
For the limit to exist, the right- and left-hand limits must exist and be equal. Thus,
ii.)
![]() ,
,
so that
2A - 2B = 2 ,
or
(Equation 1)
A - B = 1 .
Now consider continuity at x=1 . Function f must be defined at x=1 , so
i.) f(1)= 2(1)2 + 3A(1) + B = 2 + 3A + B .
The left-hand limit
![]() =
=
![]()
= 2(1)2 + 3A(1) + B
= 2 + 3A + B .
The right-hand limit
![]() =
=
![]()
= 4 .
For the limit to exist, the right- and left-hand limits must exist and be equal. Thus,
ii.)
![]() ,
,
or
(Equation 2)
3A + B = 2 .
Now solve Equations 1 and 2 simultaneously. Thus,
A - B = 1 and 3A + B = 2
are equivalent to
A = B + 1 and 3A + B = 2 .
Use the first equation to substitute into the second, getting
3 (B + 1 ) + B = 2 ,
3 B + 3 + B = 2 ,
and
4 B = -1 .
Thus,
![]()
and
![]() .
.
For this choice of A and B it can easily be shown that
iii.)
![]()
and
iii.)
![]() ,
,
so that all three conditions are satisfied at both x=1 and x=-1 , and function f is continuous at both x=1 and x=-1 . Therefore, function f is continuous for all values of x if
![]() and
and
![]() .
.
Click HERE to return to the list of problems.
SOLUTION 14 : First describe f using functional composition. Let g(x) = -1/x2 and h(x) = ex . Function h is well-known to be continuous for all values of x . Function g is the quotient of functions continuous for all values of x , and is therefore continuous for all values of x except x=0 , that x which makes the denominator zero. Thus, for all values of x except x=0 ,
f(x) = h ( g(x) ) = e g(x) = e -1/x2
is a continuous function (the functional composition of continuous functions). Now check for continuity of f at x=0 . Function f is defined at x=0 since
i.) f(0) = 0 .
The limit
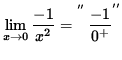
(The numerator approaches -1 and the denominator is a positive number approaching zero.)
![]() ,
,
so that
![]()
![]()
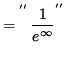
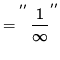
= 0 ,
i.e.,
ii.)
![]() .
.
Since
iii.)
![]() ,
,
all three conditions are satisfied, and f is continuous at x=0 . Thus, f is continuous for all values of x .
Click HERE to return to the list of problems.
SOLUTION 15 : First show that f is continuous for all values of x . Describe f using functional composition. Let
![]() ,
,
![]() , and
k(x) = x2 . Function h is well-known to be continuous for all values of x . Function k is a polynomial and is therefore continuous for all values of x . Function g is the quotient of functions continuous for all values of x , and is therefore continuous for all values of x except x=0 , that x which makes the denominator zero. Thus, for all values of x except x=0 ,
, and
k(x) = x2 . Function h is well-known to be continuous for all values of x . Function k is a polynomial and is therefore continuous for all values of x . Function g is the quotient of functions continuous for all values of x , and is therefore continuous for all values of x except x=0 , that x which makes the denominator zero. Thus, for all values of x except x=0 ,
![]()
is a continuous function (the product and functional composition of continuous functions). Now check for continuity of f at x=0 . Function f is defined at x=0 since
i.) f(0) = 0 .
The limit
![]() does not exist since the values of
does not exist since the values of
![]() oscillate between -1 and +1 as x approaches zero.
However, for
oscillate between -1 and +1 as x approaches zero.
However, for ![]()
![]()
so that
![]() .
.
Since
![]() ,
,
it follows from the Squeeze Principle that
ii.)
![]() .
.
Since
iii.)
![]() ,
,
all three conditions are satisfied, and f is continuous at x=0 . Thus, f is continuous for all values of x .
Now show that f is differentiable for all values of x . For ![]() we can differentiate f using the product rule and the chain rule. That is, for
we can differentiate f using the product rule and the chain rule. That is, for ![]() the derivative of f is
the derivative of f is
![]()
![]()
![]()
![]() .
.
Use the limit definition of the derivative to differentiate f at x=0 . Then
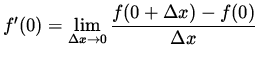
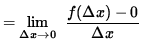
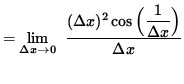
![]() .
.
Use the Squeeze Principle to evaluate this limit. For
![]()
![]() .
.
If
![]() , then
, then
![]() .
.
If
![]() , then
, then
![]() .
.
In either case,
![]() ,
,
and it follows from the Squeeze Principle that
![]() .
.
Thus, f is differentiable for all values of x . Check to see if f' is continuous at x=0 . The function f' is defined at x=0 since
i.) f'(0) = 0 .
However,
ii.)
![]()
does not exist since the values of
![]() oscillate between -1 and +1 as x approaches zero. Thus, condition ii.) is violated, and the derivative , f' , is not continuous at x=0 .
oscillate between -1 and +1 as x approaches zero. Thus, condition ii.) is violated, and the derivative , f' , is not continuous at x=0 .
NOTE : The continuity of function f for all values of x also follows from the fact that f is differentiable for all values of x .
Click HERE to return to the list of problems.