SOLUTION 25: The cube has an edge length of $30$ cm and it's frosting is $0.5$ cm thick. Recall that the volume of a cube of edge length $x$ is
$$ V = x^3 $$
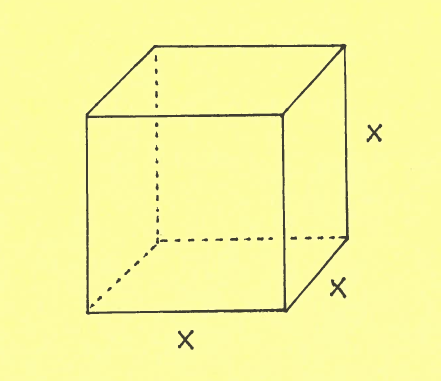
and choose
$$ x-values: 30 \rightarrow 30 +(0.5 + 0.5)= 31 $$
so that
$$ \Delta x = 31-30 = 1 $$
The derivative of $ V $ is
$$ V'= 3 x^2 $$
$ \ \ \ \ $ a.) The exact volume of the frosting is the exact change of $V-$values and is
$$ \Delta V = V(31) - V(30) $$
$$ = (31)^3 - (30)^3 $$
$$ = 29,791 - 27,000 $$
$$ = 2791 \ cm^3 $$
$ \ \ \ \ $ b.) An estimate for volume of the frosting is the Differential of $V$ (since $ \Delta V \approx dV)$ and is
$$ dV = V'(30) \ \Delta x $$
$$ = 3 (30)^2 \cdot (1) $$
$$ = 2700 \ cm^3 $$
Click HERE to return to the list of problems.

