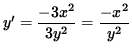 .
.
SOLUTION 1 : Begin with x3 + y3 = 4 . Differentiate both sides of the equation, getting
D ( x3 + y3 ) = D ( 4 ) ,
D ( x3 ) + D ( y3 ) = D ( 4 ) ,
(Remember to use the chain rule on D ( y3 ) .)
3x2 + 3y2 y' = 0 ,
so that (Now solve for y' .)
3y2 y' = - 3x2 ,
and
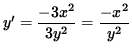 .
.
Click HERE to return to the list of problems.
SOLUTION 2 : Begin with (x-y)2 = x + y - 1 . Differentiate both sides of the equation, getting
D (x-y)2 = D ( x + y - 1 ) ,
D (x-y)2 = D ( x ) + D ( y ) - D ( 1 ) ,
(Remember to use the chain rule on D (x-y)2 .)
![]() ,
,
2 (x-y) (1- y') = 1 + y' ,
so that (Now solve for y' .)
2 (x-y) - 2 (x-y) y' = 1 + y' ,
- 2 (x-y) y' - y' = 1 - 2 (x-y) ,
(Factor out y' .)
y' [ - 2 (x-y) - 1 ] = 1 - 2 (x-y) ,
and
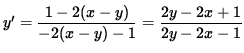 .
.
Click HERE to return to the list of problems.
SOLUTION 3 : Begin with
![]() . Differentiate both sides of the equation, getting
. Differentiate both sides of the equation, getting
![]() ,
,
(Remember to use the chain rule on
![]() .)
.)
![]() ,
,
![]() ,
,
so that (Now solve for y' .)
![]() ,
,
![]() ,
,
(Factor out y' .)
![]() ,
,
and
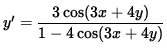 .
.
Click HERE to return to the list of problems.
SOLUTION 4 : Begin with y = x2 y3 + x3 y2 . Differentiate both sides of the equation, getting
D(y) = D ( x2 y3 + x3 y2 ) ,
D(y) = D ( x2 y3 ) + D ( x3 y2 ) ,
(Use the product rule twice.)
![]() ,
,
(Remember to use the chain rule on D ( y3 ) and D ( y2 ) .)
![]() ,
,
y' = 3x2 y2 y' + 2x y3 + 2x3 y y' + 3x2 y2 ,
so that (Now solve for y' .)
y' - 3x2 y2 y' - 2x3 y y' = 2x y3 + 3x2 y2 ,
(Factor out y' .)
y' [ 1 - 3x2 y2 - 2x3 y ] = 2x y3 + 3x2 y2 ,
and
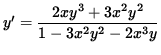 .
.
Click HERE to return to the list of problems.
SOLUTION 5 :
Begin with
![]() . Differentiate both sides of the equation, getting
. Differentiate both sides of the equation, getting
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
so that (Now solve for ![]() .)
.)
![]() ,
,
![]() ,
,
(Factor out ![]() .)
.)
![]() ,
,
and
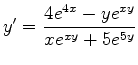 .
.
Click HERE to return to the list of problems.
SOLUTION 6 : Begin with
![]() . Differentiate both sides of the equation, getting
. Differentiate both sides of the equation, getting
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
so that (Now solve for y' .)
![]() ,
,
![]() ,
,
(Factor out y' .)
![]() ,
,
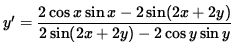 ,
,
![$ y' = \displaystyle{ 2 [ \cos x \sin x - \sin( 2x + 2y) ] \over 2 [ \sin( 2x + 2y) - \cos y \sin y ] } $](img26.gif) ,
,
and
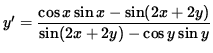 .
.
Click HERE to return to the list of problems.
SOLUTION 7 : Begin with
![]() . Differentiate both sides of the equation, getting
. Differentiate both sides of the equation, getting
![]() ,
,
1 = (1/2)( x2 + y2 )-1/2 D ( x2 + y2 ) ,
1 = (1/2)( x2 + y2 )-1/2 ( 2x + 2y y' ) ,
so that (Now solve for y' .)
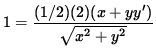 ,
,
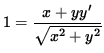 ,
,
![]() ,
,
![]() ,
,
and
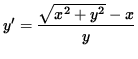 .
.
Click HERE to return to the list of problems.
SOLUTION 8 : Begin with
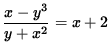 . Clear the fraction by multiplying both sides of the equation by y + x2 , getting
. Clear the fraction by multiplying both sides of the equation by y + x2 , getting
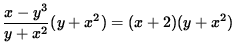 ,
,
or
x - y3 = xy + 2y + x3 + 2x2 .
Now differentiate both sides of the equation, getting
D ( x - y3 ) = D ( xy + 2y + x3 + 2x2 ) ,
D ( x ) - D (y3 ) = D ( xy ) + D ( 2y ) + D ( x3 ) + D ( 2x2 ) ,
(Remember to use the chain rule on D (y3 ) .)
1 - 3 y2 y' = ( xy' + (1)y ) + 2 y' + 3x2 + 4x ,
so that (Now solve for y' .)
1 - y - 3x2 - 4x = 3 y2 y' + xy' + 2 y' ,
(Factor out y' .)
1 - y - 3x2 - 4x = (3y2 + x + 2) y' ,
and
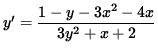 .
.
Click HERE to return to the list of problems.
SOLUTION 9 : Begin with
![]() . Clear the fractions by multiplying both sides of the equation by x3 y3 , getting
. Clear the fractions by multiplying both sides of the equation by x3 y3 , getting
![]() ,
,
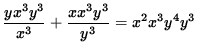 ,
,
y4 + x4 = x5 y7 .
Now differentiate both sides of the equation, getting
D ( y4 + x4 ) = D ( x5 y7 ) ,
D ( y4 ) + D ( x4 ) = x5 D (y7 ) + D ( x5 ) y7 ,
(Remember to use the chain rule on D (y4 ) and D (y7 ) .)
4 y3 y' + 4 x3 = x5 (7 y6 y' ) + ( 5 x4 ) y7 ,
so that (Now solve for y' .)
4 y3 y' - 7 x5 y6 y' = 5 x4 y7 - 4 x3 ,
(Factor out y' .)
y' [ 4 y3 - 7 x5 y6 ] = 5 x4 y7 - 4 x3 ,
and
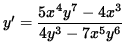 .
.
Click HERE to return to the list of problems.
SOLUTION 10 : Begin with (x2+y2)3 = 8x2y2 . Now differentiate both sides of the equation, getting
D (x2+y2)3 = D ( 8x2y2 ) ,
3 (x2+y2)2 D (x2+y2) = 8x2 D (y2 ) + D ( 8x2 ) y2 ,
(Remember to use the chain rule on D (y2 ) .)
3 (x2+y2)2 ( 2x + 2 y y' ) = 8x2 (2 y y' ) + ( 16 x ) y2 ,
so that (Now solve for y' .)
6x (x2+y2)2 + 6 y (x2+y2)2 y' = 16 x2 y y' + 16 x y2 ,
6 y (x2+y2)2 y' - 16 x2 y y' = 16 x y2 - 6x (x2+y2)2 ,
(Factor out y' .)
y' [ 6 y (x2+y2)2 - 16 x2 y ] = 16 x y2 - 6x (x2+y2)2 ,
and
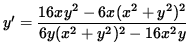 .
.
Thus, the slope of the line tangent to the graph at the point (-1, 1) is
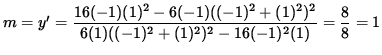 ,
,
and the equation of the tangent line is
y - ( 1 ) = (1) ( x - ( -1 ) )
or
y = x + 2 .
Click HERE to return to the list of problems.
SOLUTION 11 : Begin with x2 + (y-x)3 = 9 . If x=1 , then
(1)2 + ( y-1 )3 = 9
so that
( y-1 )3 = 8 ,
y-1 = 2 ,
y = 3 ,
and the tangent line passes through the point (1, 3) . Now differentiate both sides of the original equation, getting
D ( x2 + (y-x)3 ) = D ( 9 ) ,
D ( x2 ) + D (y-x)3 = D ( 9 ) ,
2x + 3 (y-x)2 D (y-x) = 0 ,
2x + 3 (y-x)2 (y'-1) = 0 ,
so that (Now solve for y' .)
2x + 3 (y-x)2 y'- 3 (y-x)2 = 0 ,
3 (y-x)2 y' = 3 (y-x)2 - 2x ,
and
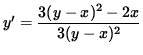 .
.
Thus, the slope of the line tangent to the graph at (1, 3) is
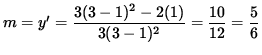 ,
,
and the equation of the tangent line is
y - ( 3 ) = (5/6) ( x - ( 1 ) ) ,
or
y = (5/6) x + (13/6) .
Click HERE to return to the list of problems.
SOLUTION 12 : Begin with x2y + y4 = 4 + 2x . Now differentiate both sides of the original equation, getting
D ( x2 y + y4 ) = D ( 4 + 2x ) ,
D ( x2 y ) + D (y4 ) = D ( 4 ) + D ( 2x ) ,
( x2 y' + (2x) y ) + 4 y3 y' = 0 + 2 ,
so that (Now solve for y' .)
x2 y' + 4 y3 y' = 2 - 2x y ,
(Factor out y' .)
y' [ x2 + 4 y3 ] = 2 - 2x y ,
and
(Equation 1)
![]() .
.
Thus, the slope of the graph (the slope of the line tangent to the graph) at (-1, 1) is
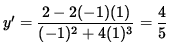 .
.
Since y'= 4/5 , the slope of the graph is 4/5 and the graph is increasing at the point (-1, 1) . Now determine the concavity of the graph at (-1, 1) . Differentiate Equation 1, getting
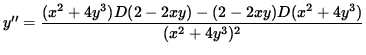
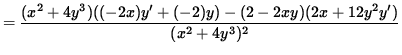 .
.
Now let x=-1 , y=1 , and y'=4/5 so that the second derivative is
![$ y'' = \displaystyle{ [(-1)^2 + 4 (1)^3][(- 2(-1))(4/5)+(- 2)(1)] - [2 - 2(-1)(1)][2(-1)+12 (1)^2(4/5)]
\over ((-1)^2 + 4(1)^3)^2 } $](img50.gif)
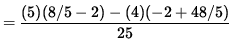
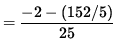
![]() .
.
Since y'' < 0 , the graph is concave down at the point (-1, 1) .
Click HERE to return to the list of problems.