.125truein ^^^^''0 0^''
SOLUTION 1: Differentiate ![]() . Apply the product rule.
Then
. Apply the product rule.
Then
![]()
![]()
(Factor an x from each term.)
![]() .
.
SOLUTION 2: Differentiate ![]() . Apply the quotient rule. Then
. Apply the quotient rule. Then
![]()
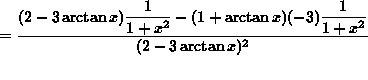
![]()
![]()
![]() .
.
SOLUTION 3: Differentiate ![]() arc
arc![]() arc
arc![]() .
Apply the product rule. Then
.
Apply the product rule. Then
![]() arc
arc![]() arc
arc![]() arc
arc![]() arc
arc![]()
![]() arc
arc![]() arc
arc![]()
= ( arc![]() arc
arc![]() .
.
SOLUTION 4: Let ![]() arc
arc![]() . Solve f'(x) = 0 for x . Begin by differentiating f . Then
. Solve f'(x) = 0 for x . Begin by differentiating f . Then
![]()
![]()
(Get a common denominator and subtract fractions.)
![]()
![]()
![]()
![]()
![]() .
.
(It is a fact that if ![]() , then A = 0 .) Thus,
, then A = 0 .) Thus,
2(x - 2)(x+2) = 0 .
(It is a fact that if AB = 0 , then A = 0 or B=0 .) It follows that
x-2 = 0 or x+2 = 0 ,
that is, the only solutions to f'(x) = 0 are
x = 2 or x = -2 .
SOLUTION 5: Let ![]() . Show that f'(x) = 0 . Conclude that
. Show that f'(x) = 0 . Conclude that
![]() . Begin by differentiating f . Then
. Begin by differentiating f . Then
![]() .
.
If f'(x) = 0 for all admissable values of x , then f must be a constant function, i.e.,
![]() for all admissable values of x ,
for all admissable values of x ,
i.e.,
![]() for all admissable values of x .
for all admissable values of x .
In particular, if x = 0 , then
![]()
i.e.,
![]() .
.
Thus, ![]() and
and ![]() for all admissable values of x .
for all admissable values of x .
SOLUTION 6: Evaluate 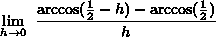 . It may not be obvious, but this problem can be viewed as a derivative problem. Recall that
. It may not be obvious, but this problem can be viewed as a derivative problem. Recall that
![]()
(Since h approaches 0 from either side of 0, h can be either a positve or a negative number. In addition,
![]() is equivalent to
is equivalent to ![]() . This explains the following
equivalent variations in the limit definition of the derivative.)
. This explains the following
equivalent variations in the limit definition of the derivative.)
![]()
![]() .
.
If ![]() , then
, then ![]() , and letting
, and letting
![]() , it follows that
, it follows that
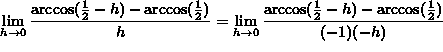
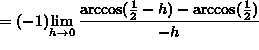
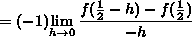
![]()
![]()
![]()
![]()
![]()
![]() .
.
The following problems require use of the chain rule.
SOLUTION 7: Differentiate ![]() . Use the product rule first. Then
. Use the product rule first. Then
![]()
(Apply the chain rule in the first summand.)
![]()
![]()
(Factor out ![]() . Then get a common denominator and add.)
. Then get a common denominator and add.)
![]()
![]()
![]() .
.
SOLUTION 8: Differentiate ![]() . Apply the chain rule twice. Then
. Apply the chain rule twice. Then
![]()
![]()
(Recall that ![]() .)
.)
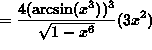
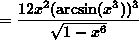 .
.
SOLUTION 9: Differentiate ![]() . Apply the chain rule twice. Then
. Apply the chain rule twice. Then
![]()
(Recall that ![]() .)
.)
![]()
![]()
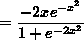 .
.
SOLUTION 10: Determine the equation of the line tangent to the graph of ![]() at x = e . If x = e , then
at x = e . If x = e , then ![]() , so that the line passes through the point
, so that the line passes through the point ![]() . The slope of the tangent line follows from the derivative (Apply the chain rule.)
. The slope of the tangent line follows from the derivative (Apply the chain rule.)
![]()
![]()
![]() .
.
The slope of the line tangent to the graph at x = e is
![]()
![]()
![]() .
.
Thus, an equation of the tangent line is
![]() .
.
SOLUTION 11: Differentiate ![]() arc
arc![]() . What conclusion can be drawn from your answer about function y ? What conclusion can be drawn about functions arc
. What conclusion can be drawn from your answer about function y ? What conclusion can be drawn about functions arc![]() and
and ![]() ? First, differentiate, applying the chain rule to the inverse cotangent function. Then
? First, differentiate, applying the chain rule to the inverse cotangent function. Then
![]()
![]()
![]()
= 0 .
If y' = 0 for all admissable values of x , then y must be a constant function, i.e.,
![]() for all admissable values of x ,
for all admissable values of x ,
i.e.,
arc![]() for all admissable values of x .
for all admissable values of x .
In particular, if x = 1 , then
arc![]()
i.e.,
![]() .
.
Thus, c = 0 and arc![]() for all admissable values of x . We conclude that
for all admissable values of x . We conclude that
arc![]() .
.
Note that this final conclusion follows even more simply and directly from the definitions of these two inverse trigonometric functions.
SOLUTION 12: Differentiate ![]() . Begin by applying the product rule to the first summand and the chain rule to the second summand. Then
. Begin by applying the product rule to the first summand and the chain rule to the second summand. Then
![]()
![]()
![]()
![]() .
.
SOLUTION 13: Find an equation of the line tangent to the graph of
![]() at x=2 . If x = 2 , then
at x=2 . If x = 2 , then ![]() , so that the line passes through the point
, so that the line passes through the point ![]() . The slope of the tangent line follows from the derivative
. The slope of the tangent line follows from the derivative
![]()
![]()
![]()
![]()
![]()
![]()
(Recall that when dividing by a fraction, one must invert and multiply by the reciprocal. That is ![]() .)
.)
![]()
![]() .
.
The slope of the line tangent to the graph at x = 2 is
![]() .
.
Thus, an equation of the tangent line is
![]()
or
![]()
or
![]() .
.
SOLUTION 14: Evaluate ![]() . Since
. Since ![]() and
and ![]() , it follows that
, it follows that
![]() takes the indeterminate form . Thus, we can apply
L'H
takes the indeterminate form . Thus, we can apply
L'H![]() pital's Rule. Begin by differentiating the numerator and denominator separately. DO NOT apply the quotient rule ! Then
pital's Rule. Begin by differentiating the numerator and denominator separately. DO NOT apply the quotient rule ! Then
![]() =
= 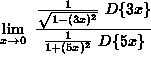
= 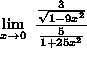
(Recall that when dividing by a fraction, one must invert and multiply by the reciprocal. That is 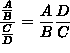 .)
.)
= 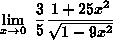
= ![]()
= ![]() .
.
SOLUTION 15: A movie screen on the front wall in your classroom is 16 feet high and positioned 9 feet above your eye-level. How far away from the front of the room should you sit in order to have the ``best" view ? Begin by introducing variables x and ![]() . (See the diagram below.)
. (See the diagram below.)
From trigonometry it follows that
![]() ,
,
so that
![]() .
.
In addition,
![]()
so that
![]() .
.
It follows that
![]()
![]() ,
,
that is, angle ![]() is explicitly a function of distance x . Now find the value of x which maximizes the value of function
is explicitly a function of distance x . Now find the value of x which maximizes the value of function ![]() . Begin by differentiating function
. Begin by differentiating function ![]() and setting the derivative equal to zero. Then
and setting the derivative equal to zero. Then
![]()
![]()
![]() .
.
![]() .
.
Now solve this equation for x . Then
![]()
iff
![]()
iff
![]()
iff
![]()
iff
![]()
iff
![]() feet .
feet .
Use the first or second derivative test (The first derivative test is easier.) to verify that this value of x
determines a maximum value for ![]() .
.