.125truein ^^^^''0 0^''

SOLUTION 1: Differentiate . Apply the product rule. Then

(Factor an x from each term.)

.

SOLUTION 2: Differentiate . Apply the quotient rule. Then

.

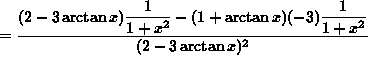
SOLUTION 3: Differentiate arcarc . Apply the product rule. Then

arcarcarcarc

arcarc

= ( arcarc .

SOLUTION 4: Let arc . Solve f'(x) = 0 for x . Begin by differentiating f . Then

(Get a common denominator and subtract fractions.)

.

(It is a fact that if , then A = 0 .) Thus,

2(x - 2)(x+2) = 0 .

(It is a fact that if AB = 0 , then A = 0 or B=0 .) It follows that

x-2 = 0 or x+2 = 0 ,

that is, the only solutions to f'(x) = 0 are

x = 2 or x = -2 .

SOLUTION 5: Let . Show that f'(x) = 0 . Conclude that . Begin by differentiating f . Then

.

If f'(x) = 0 for all admissable values of x , then f must be a constant function, i.e.,

for all admissable values of x ,

i.e.,

for all admissable values of x .

In particular, if x = 0 , then

i.e.,

.

Thus, and for all admissable values of x .

SOLUTION 6: Evaluate 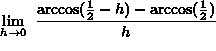. It may not be obvious, but this problem can be viewed as a derivative problem. Recall that

(Since h approaches 0 from either side of 0, h can be either a positve or a negative number. In addition, is equivalent to . This explains the following equivalent variations in the limit definition of the derivative.)

.

If , then , and letting , it follows that

.

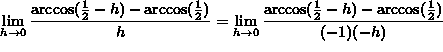
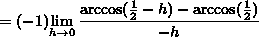
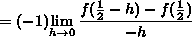
The following problems require use of the chain rule.

SOLUTION 7: Differentiate . Use the product rule first. Then

(Apply the chain rule in the first summand.)

(Factor out . Then get a common denominator and add.)

.

SOLUTION 8: Differentiate . Apply the chain rule twice. Then

(Recall that .)

.

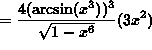
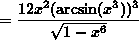SOLUTION 9: Differentiate . Apply the chain rule twice. Then

(Recall that .)

.

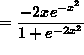SOLUTION 10: Determine the equation of the line tangent to the graph of at x = e . If x = e , then , so that the line passes through the point . The slope of the tangent line follows from the derivative (Apply the chain rule.)

.

The slope of the line tangent to the graph at x = e is

.

Thus, an equation of the tangent line is

.

SOLUTION 11: Differentiate arc . What conclusion can be drawn from your answer about function y ? What conclusion can be drawn about functions arc and ? First, differentiate, applying the chain rule to the inverse cotangent function. Then

= 0 .

If y' = 0 for all admissable values of x , then y must be a constant function, i.e.,

for all admissable values of x ,

i.e.,

arc for all admissable values of x .

In particular, if x = 1 , then

arc

i.e.,

.

Thus, c = 0 and arc for all admissable values of x . We conclude that

arc .

Note that this final conclusion follows even more simply and directly from the definitions of these two inverse trigonometric functions.

SOLUTION 12: Differentiate . Begin by applying the product rule to the first summand and the chain rule to the second summand. Then

.

SOLUTION 13: Find an equation of the line tangent to the graph of at x=2 . If x = 2 , then , so that the line passes through the point . The slope of the tangent line follows from the derivative

(Recall that when dividing by a fraction, one must invert and multiply by the reciprocal. That is .)

.

The slope of the line tangent to the graph at x = 2 is

.

Thus, an equation of the tangent line is

or

or

.

SOLUTION 14: Evaluate . Since and , it follows that takes the indeterminate form . Thus, we can apply L'Hpital's Rule. Begin by differentiating the numerator and denominator separately. DO NOT apply the quotient rule ! Then

=

=

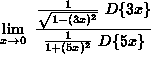
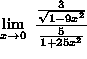
(Recall that when dividing by a fraction, one must invert and multiply by the reciprocal. That is .)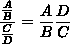

=

=

= .

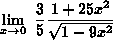
SOLUTION 15: A movie screen on the front wall in your classroom is 16 feet high and positioned 9 feet above your eye-level. How far away from the front of the room should you sit in order to have the ``best" view ? Begin by introducing variables x and . (See the diagram below.)

From trigonometry it follows that

,

so that

.

In addition,

so that

.

It follows that

,

that is, angle is explicitly a function of distance x . Now find the value of x which maximizes the value of function . Begin by differentiating function and setting the derivative equal to zero. Then

.

.

Now solve this equation for x . Then

iff

iff

iff

iff

iff

feet .

Use the first or second derivative test (The first derivative test is easier.) to verify that this value of x determines a maximum value for .

 
• About this document ...