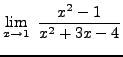 =
=
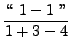 =
=
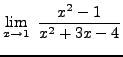 =
=
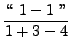 =
=
![]()
(Apply Theorem 1 for l'Hopital's Rule. Differentiate top and bottom separately.)
=
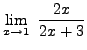
truein
=
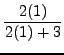
truein
=
![]() .
truein
truein
SOLUTION 2:
.
truein
truein
SOLUTION 2:
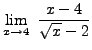 =
=
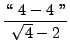 =
=
![]() truein
(Apply Theorem 1 for l'Hopital's Rule. Differentiate top and bottom separately.)
truein
truein
(Apply Theorem 1 for l'Hopital's Rule. Differentiate top and bottom separately.)
truein
=
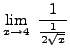
truein
=
![]()
truein
=
![]()
truein
= ![]() .
.
truein
truein
SOLUTION 3:
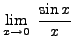 =
=
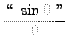 =
=
![]() truein
(Apply Theorem 1 for l'Hopital's Rule. Differentiate top and bottom separately.)
truein
truein
(Apply Theorem 1 for l'Hopital's Rule. Differentiate top and bottom separately.)
truein
=
![]()
truein
=
![]()
truein
=
![]() .
.
truein
truein
SOLUTION 4:
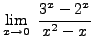 =
=
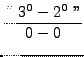 =
=
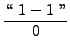 =
=
![]() truein
(Apply Theorem 1 for l'Hopital's Rule. Differentiate top and bottom separately. Recall that
truein
(Apply Theorem 1 for l'Hopital's Rule. Differentiate top and bottom separately. Recall that
![]() .)
truein
.)
truein
=
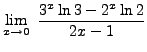
truein
=
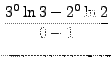
truein
=
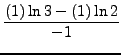
truein
=
![]()
truein
(Recall that
![]() .)
truein
truein
.)
truein
truein
=
![]() .
truein
truein
SOLUTION 5:
.
truein
truein
SOLUTION 5:
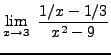 =
=
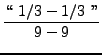 =
=
![]() truein
(Apply THEOREM 1 for l'Hopital's Rule. Differentiate top and bottom separately.)
truein
truein
(Apply THEOREM 1 for l'Hopital's Rule. Differentiate top and bottom separately.)
truein
=
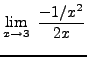
truein
=
![]()
truein
=
![]()
truein
=
![]()
truein
=
![]() .
.
truein truein
SOLUTION 6:
![]() =
=
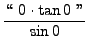 =
=
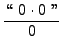 =
=
![]() truein
(Apply Theorem 1 for l'Hopital's Rule. Differentiate the top using the product rule and the bottom using the chain rule.)
truein
truein
(Apply Theorem 1 for l'Hopital's Rule. Differentiate the top using the product rule and the bottom using the chain rule.)
truein
=
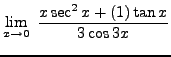
truein
=
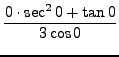
truein
=
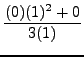
truein
=
![]()
truein
=
![]() .
.
truein
truein
SOLUTION 7:
 =
=
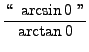 =
=
![]() truein
(Apply Theorem 1 for l'Hopital's Rule. Differentiate the top using the chain rule and the bottom using the chain rule. Recall that
truein
(Apply Theorem 1 for l'Hopital's Rule. Differentiate the top using the chain rule and the bottom using the chain rule. Recall that
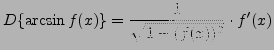 and
and
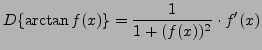 .)
truein
.)
truein
=
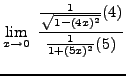
truein
=
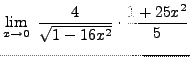
truein
=
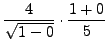
truein
=
![]() .
.
truein
truein
SOLUTION 8:
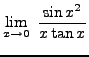 =
=
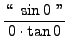 =
=
![]() =
=
![]() truein
(Apply Theorem 1 for l'Hopital's Rule. Differentiate the top using the chain rule and the bottom using the product rule.)
truein
truein
(Apply Theorem 1 for l'Hopital's Rule. Differentiate the top using the chain rule and the bottom using the product rule.)
truein
=
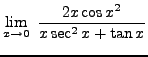
truein
=
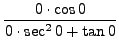 =
=
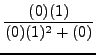 =
=
![]()
truein (Apply Theorem 1 for l'Hopital's Rule again. Differentiate the top using the product rule and the chain rule and the bottom using the product rule and the chain rule.) truein
=

truein
=
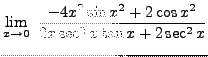
truein
=
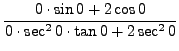
truein
=
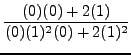
truein
=
![]()
truein
=
![]() .
.
truein
truein
SOLUTION 9:
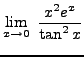 =
=
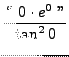 =
=
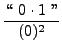 =
=
![]() truein
(Apply Theorem 1 for l'Hopital's Rule. Differentiate the top using the product rule and the bottom using the chain rule.)
truein
truein
(Apply Theorem 1 for l'Hopital's Rule. Differentiate the top using the product rule and the bottom using the chain rule.)
truein
=
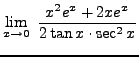
truein
=
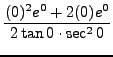 =
=
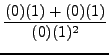 =
=
![]()
truein (Apply Theorem 1 for l'Hopital's Rule again. Differentiate the top using the product rule and the bottom using the product rule and the chain rule.) truein
=
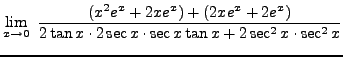
truein
=
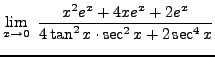
truein
=
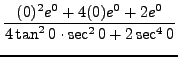
truein
=
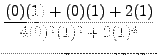
truein
=
![]()
truein
= ![]() .
.
truein
truein
SOLUTION 10:
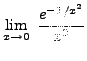 =
=
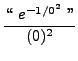
truein
=
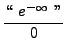 =
=
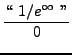 =
=
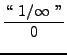 =
=
![]()
truein
(Apply Theorem 1 for l'Hopital's Rule. Differentiate the top using the chain rule and the bottom. Recall that
![]() .)
truein
.)
truein
=
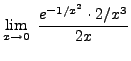
truein
=
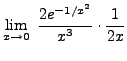
truein
=
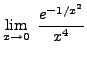 =
=
![]() .
.
truein
(Applying Theorem 1 for l'Hopital's Rule again leads to
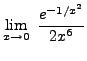 . Stop and think. This is getting nowhere. Go back to the beginning and algebraically rewrite the problem by ``flipping" both numerator and denominator.)
. Stop and think. This is getting nowhere. Go back to the beginning and algebraically rewrite the problem by ``flipping" both numerator and denominator.)
truein
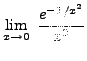 =
=
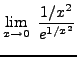
truein
=
 =
=
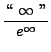 =
=
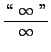
truein (Apply Theorem 2 for l'Hopital's Rule.) truein
=
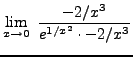
truein
=
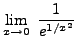
truein
=
![]()
truein
= ![]() .
.
truein
truein
SOLUTION 11:
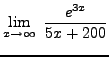 =
=
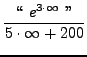 =
=
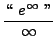 =
=
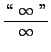
truein (Apply Theorem 2 for l'Hopital's Rule. Differentiate the top using the chain rule and the bottom.) truein
=
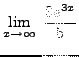
truein
=
![]()
truein
=
![]()
truein
=
![]() (So limit does not exist.).
(So limit does not exist.).
truein
truein
SOLUTION 12:
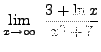 =
=
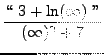 =
=
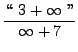 =
=
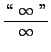
truein (Apply Theorem 2 for l'Hopital's Rule. Differentiate the top and the bottom.) truein
=
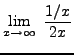
truein
=
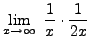
truein
=
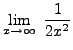
truein
=
![]()
truein
=
![]() .
.
truein
truein
SOLUTION 13:
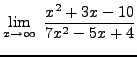 =
=
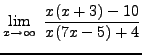
truein
=
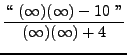 =
=
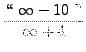 =
=
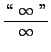
truein (Apply Theorem 2 for l'Hopital's Rule. Differentiate the top and the bottom.) truein
=
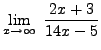
truein
=
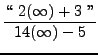 =
=
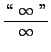
truein (Apply Theorem 2 for l'Hopital's Rule again.) truein
truein
=
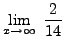
truein
=
![]() .
.
truein
truein
SOLUTION 14:
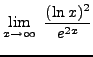 =
=
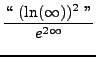 =
=
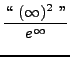 =
=
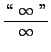
truein (Apply Theorem 2 for l'Hopital's Rule. Differentiate the top and the bottom using the chain rule.) truein
=
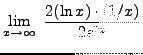
truein
=
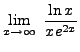
truein
=
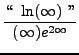 =
=
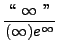 =
=
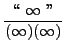 =
=
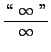
truein (Apply Theorem 2 for l'Hopital's Rule again.) truein
=
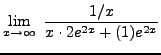
truein
=
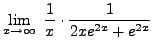
truein
=
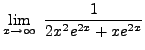
truein
=
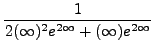
truein
=
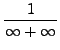
truein
=
![]() truein
truein
=
![]() .
.
truein
truein
SOLUTION 15:
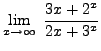 =
=
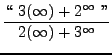 =
=
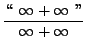 =
=
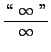
truein (Apply Theorem 2 for l'Hopital's Rule. Differentiate the top and the bottom.) truein
=
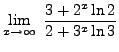
truein
=
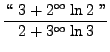 =
=
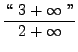 =
=
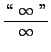
truein (Apply Theorem 2 for l'Hopital's Rule again.)
truein
=
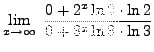
truein
=
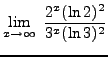
truein
=
 =
=
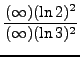 =
=
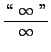
truein
(Applying Theorem 2 for l'Hopital's Rule again will lead to
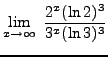 . Stop and think. This is going nowhere. There is an easy way out.)
. Stop and think. This is going nowhere. There is an easy way out.)
truein
=
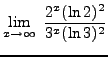
truein
=
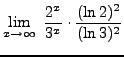
truein
=
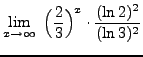
truein
=
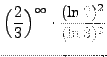
truein
=
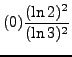
truein
=
![]() .
.
truein
truein
SOLUTION 16:
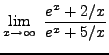 =
=
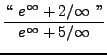 =
=
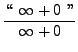 =
=
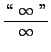
truein (Apply Theorem 2. Differentiate the top and the bottom.) truein
=
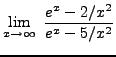 =
=
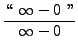 =
=
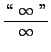
truein (Applying Theorem 2 for l'Hopital's Rule again will get us nowhere. Stop and think. Go back to the original problem and rewrite it.) truein
=
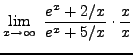
truein
=
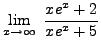 =
=
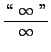
truein (Apply Theorem 2 for l'Hopital's Rule. Differentiate the top and bottom using the product rule.)
truein
=
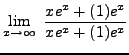
truein
=
![]()
truein
=
![]() .
.
truein
truein
SOLUTION 17:
![]() =
=
![]()
truein (Rewrite the expression by using a conjugate to circumvent this indeterminate form.) truein
=
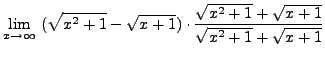
truein
(Recall that
![]() .)
truein
.)
truein
=
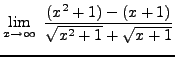
truein
=
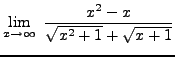
truein
=
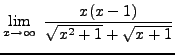 =
=
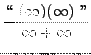 =
=
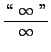
truein (Apply Theorem 2 for l'Hopital's Rule. Use the chain rule in the bottom.) truein
=
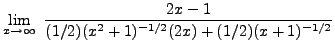
truein
=
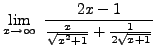
truein
=
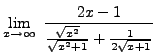
truein
=
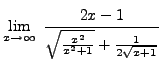
truein
=
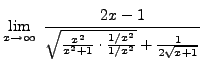
truein
=
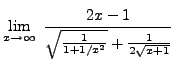
truein
=
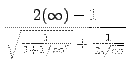
truein
=
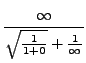
truein
=
![]()
truein
=
![]() (The limit does not exist.) .
(The limit does not exist.) .
truein
truein
SOLUTION 18:
![]() =
=
![]() =
=
![]()
truein
(This is an indeterminate form. ``Flip" ![]() so that l'Hopital's Rule can be applied.)
truein
so that l'Hopital's Rule can be applied.)
truein
=
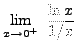 =
=
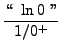 =
=
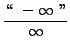
truein (Apply Theorem 2 for l'Hopital's Rule. Differentiate the top and the bottom separately.) truein
=
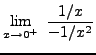
truein
=
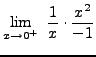
truein
=
![]()
truein
= ![]() .
.
truein
truein
SOLUTION 19:
![]() =
=
![]() =
=
![]() =
=
![]()
truein
(This is an indeterminate form. ``Flip" ![]() so that l'Hopital's Rule can be applied.)
truein
so that l'Hopital's Rule can be applied.)
truein
=
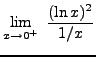 =
=
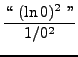 =
=
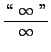
truein (Apply Theorem 2 for l'Hopital's Rule.) truein
=
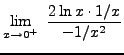
truein
=
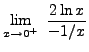 =
=
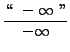
truein (Apply Theorem 2 for l'Hopital's Rule again.) truein
=
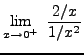
truein
=
![]()
truein
= ![]() .
.
truein
truein
SOLUTION 20:
![]() =
=
![]() =
=
![]()
truein
(Rewrite the expression to circumvent this indeterminate form. Recall that
![]() .)
truein
.)
truein
=
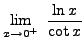 =
=
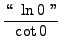 =
=
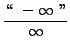
truein (Apply Theorem 2 for l'Hopital's Rule.) truein
=
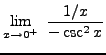
truein
(Recall that
![]() .)
truein
.)
truein
=
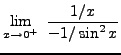
truein
=
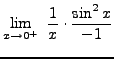
truein
=
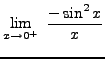 =
=
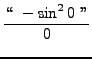 =
=
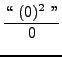 =
=
![]()
truein (Apply Theorem 1 for l'Hopital's Rule.)
truein
=
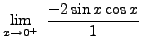
truein
=
![]()
truein
=
![]()
truein
=
![]() .
.
truein
truein
SOLUTION 21:
![]() =
=
![]() =
=
![]()
truein
(Rewrite the problem to circumvent this indeterminate form. Recall that
![]() )
truein
)
truein
=
![]()
truein
=
![]()
truein
=
![]() =
=
![]() =
=
![]()
truein
(``Flip" ![]() to circumvent this indeterminate form.)
truein
to circumvent this indeterminate form.)
truein
=
![]()
truein
=
![]() =
=
![]() =
=
![]()
truein (Apply Theorem 2 for l'Hopital's Rule.) truein
=
![]()
truein
=
![]()
truein
=
![]() =
=
![]() =
=
![]() =
=
![]()
truein (Apply Theorem 1 for l'Hopital's Rule.) truein
=
![]()
truein
=
![]()
truein
=
![]()
truein
=
![]()
truein
= ![]() .
.
truein
truein
SOLUTION 22:
![]() =
=
![]() =
=
![]()
truein
(Rewrite the problem to circumvent this indeterminate form. Recall that
![]() )
truein
)
truein
=
![]()
truein
=
![]()
truein
=
![]() =
=
![]() =
=
![]()
truein
(``Flip" ![]() to circumvent this indeterminate form.)
truein
to circumvent this indeterminate form.)
truein
=
![]() =
=
![]() =
=
![]()
truein
(Apply Theorem 1 for l'Hopital's Rule. Recall that
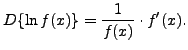 )
truein
)
truein
=
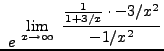
truein
=
![]()
truein
=
![]()
truein
=
![]() .
.
truein
truein
SOLUTION 23:
![]() =
=
![]() =
=
![]()
truein
(Rewrite the problem to circumvent this indeterminate form. Recall that
![]() )
truein
)
truein
=
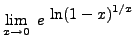
truein
=
![]()
truein
=
![]() =
=
![]() =
=
![]()
truein (Apply Theorem 1 for l'Hopital's Rule.) truein
=
![]()
truein
=
![]()
truein
=
![]()
truein
=
![]() .
.
truein
truein
SOLUTION 24:
![]() =
=
![]() =
=
![]()
truein
(Rewrite the problem to circumvent this indeterminate form. Recall that
![]() )
truein
)
truein
=
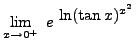
truein
=
![]()
truein
=
![]()
truein
=
![]() =
=
![]() =
=
![]()
truein
(``Flip" ![]() to circumvent this indeterminate form.)
truein
to circumvent this indeterminate form.)
truein
=
![]()
truein
=
![]() =
=
![]() =
=
![]()
truein (Apply Theorem 2 for l'Hopital's Rule.) truein
=
![]()
truein
=
![]()
truein
=
![]()
truein
=
![]() =
=
![]() =
=
![]()
truein (Apply Theorem 1 for l'Hopital's Rule.) truein
=
![]()
truein
=
![]()
truein
=
![]()
truein
=
![]()
truein
=
![]()
truein
=
![]()
truein
= ![]() .
.
truein
truein
SOLUTION 25:
![]() =
=
![]() =
=
![]()
truein
(Rewrite the problem to circumvent this indeterminate form. Recall that
![]() )
truein
)
truein
=
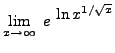
truein
=
![]()
truein
=
![]()
truein
=
![]() =
=
![]() =
=
![]()
truein (Apply Theorem 2 for l'Hopital's Rule.) truein
=
![]()
truein
=
![]()
truein
=
![]()
truein
=
![]()
truein
=
![]()
truein
=
![]()
truein
=
![]() .
.
truein
truein
SOLUTION 26:
![]() =
=
![]() =
=
![]()
truein
(Rewrite the problem to circumvent this indeterminate form. Recall that
![]() )
truein
)
truein
=
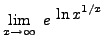
truein
=
![]()
truein
=
![]()
truein
=
![]() =
=
![]() =
=
![]()
truein (Apply Theorem 2 for l'Hopital's Rule.) truein
=
![]()
truein
=
![]()
truein
=
![]()
truein
=
![]() .
.
truein
truein
SOLUTION 27:
![]() =
=
![]()
truein
(Rewrite the problem to circumvent this indeterminate form. Recall that
![]() )
truein
)
truein
=
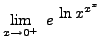
truein
=
![]()
truein
=
![]()
truein
=
![]()
truein (See Example 4 in the material preceeding this problem set.) truein
=
![]() truein
truein
=
![]()
truein
=
![]()
truein
=
![]()
truein
=
![]() .
.
truein
truein
SOLUTION 28: a.) Start with
![]() ,
truein
so that
,
truein
so that
truein
![]()
truein
and (Assume that ![]() .)
.)
truein
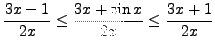 .
.
truein
Then
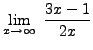 =
=
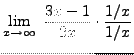
truein
=
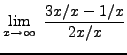
truein
=
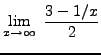
truein
=
![]()
truein
=
![]() .
.
truein
Similarly,
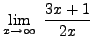 =
=
![]() .
.
truein Since
truein
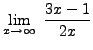 =
=
![]() =
=
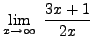 ,
,
truein it follows from the Squeeze Principle that
truein
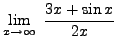 =
=
![]() .
.
truein
truein
SOLUTION 28: b.)
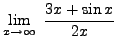 =
=
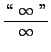
truein (Apply Theorem 2 for l'Hopital's Rule.) truein
=
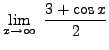
truein which does not exist since truein
![]() .
.
truein
truein
SOLUTION 28: c.) The answers to parts a.) and b.) tell us that l'Hopital's Rule may give us a wrong answer if the answer is `` does not exist." We can only be sure that l'Hopital's Rule gives us the correct answer if the answer is finite, ![]() , or
, or ![]() .
.