SOLUTIONS TO LIMITS OF FUNCTIONS AS X APPROACHES PLUS OR MINUS INFINITY



SOLUTION 1 :

tex2html_wrap_inline288 = tex2html_wrap_inline290 = 0 .

(The numerator is always 100 and the denominator tex2html_wrap_inline294 approaches tex2html_wrap_inline296 as x approaches tex2html_wrap_inline296 , so that the resulting fraction approaches 0.)

Click HERE to return to the list of problems.




SOLUTION 2 :

tex2html_wrap_inline300 = tex2html_wrap_inline302 = 0 .

(The numerator is always 7 and the denominator tex2html_wrap_inline306 approaches tex2html_wrap_inline308 as x approaches tex2html_wrap_inline308 , so that the resulting fraction approaches 0.)

Click HERE to return to the list of problems.




SOLUTION 3 :

tex2html_wrap_inline312 = tex2html_wrap_inline314

(This is NOT equal to 0. It is an indeterminate form. It can be circumvented by factoring.)

tex2html_wrap_inline316

(As x approaches tex2html_wrap_inline296 , each of the two expressions tex2html_wrap_inline320 and 3 x - 1000 approaches tex2html_wrap_inline296 .)

= tex2html_wrap_inline326

(This is NOT an indeterminate form. It has meaning.)

= tex2html_wrap_inline296 .

(Thus, the limit does not exist. Note that an alternate solution follows by first factoring out tex2html_wrap_inline330 , the highest power of x . Try it.)

Click HERE to return to the list of problems.




SOLUTION 4 :

tex2html_wrap_inline334 = tex2html_wrap_inline336

(As x approaches tex2html_wrap_inline308 , each of the two expressions tex2html_wrap_inline340 and tex2html_wrap_inline342 approaches tex2html_wrap_inline296 . )

= tex2html_wrap_inline346

(This is NOT an indeterminate form. It has meaning.)

= tex2html_wrap_inline296 .

(Thus, the limit does not exist. Note that an alternate solution follows by first factoring out tex2html_wrap_inline340 , the highest power of x . Try it.)

Click HERE to return to the list of problems.




SOLUTION 5 :

tex2html_wrap_inline354

(Note that the expression tex2html_wrap_inline356 leads to the indeterminate form tex2html_wrap_inline314 . Circumvent this by appropriate factoring.)

= tex2html_wrap_inline360 .

(As x approaches tex2html_wrap_inline296 , each of the three expressions tex2html_wrap_inline320 , tex2html_wrap_inline366 , and x - 10 approaches tex2html_wrap_inline296 .)

= tex2html_wrap_inline372

= tex2html_wrap_inline346

= tex2html_wrap_inline296 .

(Thus, the limit does not exist. Note that an alternate solution follows by first factoring out tex2html_wrap_inline378 , the highest power of x . Try it. )

Click HERE to return to the list of problems.




SOLUTION 6 :

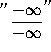
tex2html_wrap_inline382 = tex2html_wrap_inline384

(This is an indeterminate form. Circumvent it by dividing each term by x .)

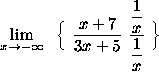
= tex2html_wrap_inline388

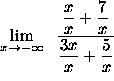
= tex2html_wrap_inline390

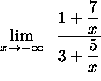
= tex2html_wrap_inline392

(As x approaches tex2html_wrap_inline308 , each of the two expressions tex2html_wrap_inline398 and tex2html_wrap_inline400 approaches 0.)

= tex2html_wrap_inline402

= tex2html_wrap_inline404 .

Click HERE to return to the list of problems.




SOLUTION 7 :

tex2html_wrap_inline406

(Note that the expression tex2html_wrap_inline408 leads to the indeterminate form tex2html_wrap_inline314 as x approaches tex2html_wrap_inline296 . Circumvent this by dividing each of the terms in the original problem by tex2html_wrap_inline320 .)

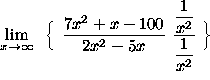
= tex2html_wrap_inline416

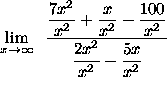
= tex2html_wrap_inline418

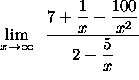
= tex2html_wrap_inline420

(Each of the three expressions tex2html_wrap_inline422 , tex2html_wrap_inline424 , and tex2html_wrap_inline400 approaches 0 as x approaches tex2html_wrap_inline296 .)

= tex2html_wrap_inline434

= tex2html_wrap_inline436 .

Click HERE to return to the list of problems.




SOLUTION 8 :

tex2html_wrap_inline438

(Note that the expression tex2html_wrap_inline440 leads to the indeterminate form tex2html_wrap_inline314 as x approaches tex2html_wrap_inline296 . Circumvent this by dividing each of the terms in the original problem by tex2html_wrap_inline330 , the highest power of x in the problem . This is not the only step that will work here. Dividing by tex2html_wrap_inline320 , the highest power of x in the numerator, also leads to the correct answer. You might want to try it both ways to convince yourself of this.)

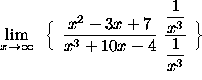
= tex2html_wrap_inline456

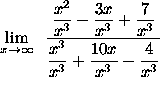
= tex2html_wrap_inline458

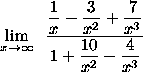
= tex2html_wrap_inline460

(Each of the five expressions tex2html_wrap_inline422 , tex2html_wrap_inline464 , tex2html_wrap_inline466 , tex2html_wrap_inline468 , and tex2html_wrap_inline470 approaches 0 as x approaches tex2html_wrap_inline296 .)

= tex2html_wrap_inline478

= 0 .

Click HERE to return to the list of problems.




SOLUTION 9 :

tex2html_wrap_inline482

(Note that the expression tex2html_wrap_inline484 leads to the indeterminate form tex2html_wrap_inline314 as x approaches tex2html_wrap_inline308 . Circumvent this by dividing each of the terms in the original problem by tex2html_wrap_inline320 , the highest power of x in the problem. . This is not the only step that will work here. Dividing by x , the highest power of x in the denominator, actually leads more easily to the correct answer. You might want to try it both ways to convince yourself of this.)

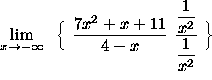
= tex2html_wrap_inline500

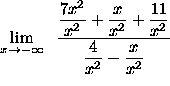
= tex2html_wrap_inline502

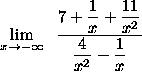
= tex2html_wrap_inline504

(Each of the three expressions tex2html_wrap_inline422 , tex2html_wrap_inline508 , and tex2html_wrap_inline510 approaches 0 as x approaches tex2html_wrap_inline308 .)

= tex2html_wrap_inline518

= tex2html_wrap_inline520

(This is NOT an indeterminate form. It has meaning. However, to determine it's exact meaning requires a bit more analysis of the origin of the 0 in the denominator. Note that tex2html_wrap_inline522 = tex2html_wrap_inline524 . It follows that if x is a negative number then both of the expressions tex2html_wrap_inline422 and tex2html_wrap_inline530 are negative so that tex2html_wrap_inline524 is positive. 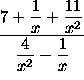Thus, for the expression tex2html_wrap_inline534 the numerator approaches 7 and the denominator is a positive quantity approaching 0 as x approaches tex2html_wrap_inline308 . The resulting limit is tex2html_wrap_inline296 .)

= tex2html_wrap_inline296 .

(Thus, the limit does not exist.)

Click HERE to return to the list of problems.




SOLUTION 10 :

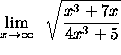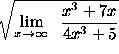
tex2html_wrap_inline544 = tex2html_wrap_inline546

(You will learn later that the previous step is valid because of the continuity of the square root function.)

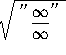
= tex2html_wrap_inline548

(Inside the square root sign lies an indeterminate form. Circumvent it by dividing each term by tex2html_wrap_inline330 , the highest power of x inside the square root sign.)

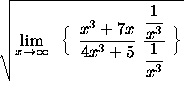
= tex2html_wrap_inline554

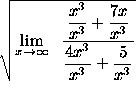
= tex2html_wrap_inline556

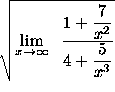
= tex2html_wrap_inline558

(Each of the two expressions tex2html_wrap_inline560 and tex2html_wrap_inline562 approaches 0 as x approaches tex2html_wrap_inline296 .)

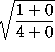
= tex2html_wrap_inline570

= tex2html_wrap_inline572

= tex2html_wrap_inline574 .

Click HERE to return to the list of problems.




SOLUTION 11 :

tex2html_wrap_inline576 = `` tex2html_wrap_inline578 ''

(Circumvent this indeterminate form by using the conjugate of the expression tex2html_wrap_inline580 in an appropriate fashion.)

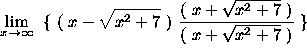
= tex2html_wrap_inline582

(Recall that tex2html_wrap_inline584 .)

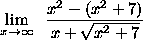
= tex2html_wrap_inline586

= tex2html_wrap_inline588

= tex2html_wrap_inline590

= tex2html_wrap_inline592

= 0 .

Click HERE to return to the list of problems.




SOLUTION 12 :

tex2html_wrap_inline596 = tex2html_wrap_inline598

(This is NOT an indeterminate form. It has meaning.)

= tex2html_wrap_inline308 .

(Thus, the limit does not exist.)

Click HERE to return to the list of problems.





Duane Kouba
Wed Apr 2 17:33:41 PST 1997