if ![]() , then
, then ![]() .
.
In general, the value of ![]() will depend on the value of
will depend on the value of ![]() . That is, we will always begin with
. That is, we will always begin with ![]() and then determine an appropriate corresponding value for
and then determine an appropriate corresponding value for ![]() . There are many values of
. There are many values of ![]() which work. Once you find a value that works, all smaller values of
which work. Once you find a value that works, all smaller values of ![]() also work.
also work.
To try and understand the meaning behind this abstract definition, see the given diagram below.
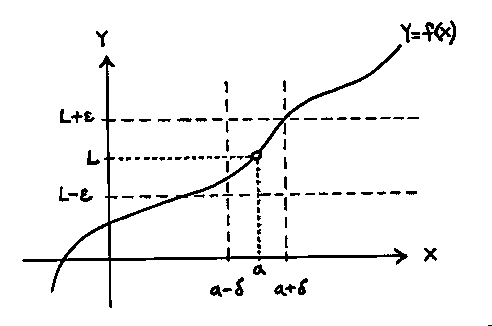
We first pick an ![]() band around the number L on the y-axis . We then determine a
band around the number L on the y-axis . We then determine a ![]() band around the number a on the x-axis so that for all x-values (excluding x=a ) inside the
band around the number a on the x-axis so that for all x-values (excluding x=a ) inside the ![]() band, the corresponding y-values lie inside the
band, the corresponding y-values lie inside the ![]() band. In other words, we first pick a prescribed closeness (
band. In other words, we first pick a prescribed closeness (![]() ) to L . Then we get close enough (
) to L . Then we get close enough (![]() ) to a so that all the corresponding y-values fall inside the
) to a so that all the corresponding y-values fall inside the ![]() band.
If a
band.
If a ![]() can be found for each value of
can be found for each value of ![]() , then we have proven that
L is the correct limit. If there is a single
, then we have proven that
L is the correct limit. If there is a single ![]() for which this process fails, then the limit L has been incorrectly computed, or the limit does not exist.
for which this process fails, then the limit L has been incorrectly computed, or the limit does not exist.
In the problems that follow, we will use this precise definition to mathematically PROVE that the limits we compute algebraically are correct. When using this definition, begin each proof by letting ![]() be given. Then take the expression
be given. Then take the expression ![]() and, from this, attempt to algebraically ``solve for" | x - a | . At that point, an appropriate value for
and, from this, attempt to algebraically ``solve for" | x - a | . At that point, an appropriate value for ![]() can easily be determined.
can easily be determined.
The expression `` iff " will be used often in the solutions to the following problems. It means `` if and only if " or `` is equivalent to ''. The expression `` min{A, B }" will also be used in many of the solutions. It means `` the minimum value of A and B." For example, min{ 3, 7 } = 3.
Click HERE to see a detailed solution to problem 1.
Click HERE to see a detailed solution to problem 2.
Click HERE to see a detailed solution to problem 3.
Click HERE to see a detailed solution to problem 4.
Click HERE to see a detailed solution to problem 5.
Click HERE to see a detailed solution to problem 6.
Click HERE to see a detailed solution to problem 7.
Click HERE to see a detailed solution to problem 8.
Click HERE to see a detailed solution to problem 9.
Click HERE to see a detailed solution to problem 10.
Click HERE to see a detailed solution to problem 11.
Click HERE to see a detailed solution to problem 12.
Click HERE to see a detailed solution to problem 13.
Click HERE to see a detailed solution to problem 14.
![]()
for any two real numbers A and B .
Click HERE to see a detailed solution to problem 15.
Your comments and suggestions are welcome. Please e-mail any correspondence to Duane Kouba by clicking on the following address :