![]() .
.
Remember the rule in the following way. Always start with the ``bottom'' function and end with the ``bottom'' function squared. Note that the numerator of the quotient rule is identical to the ordinary product rule except that subtraction replaces addition. In the list of problems which follows, most problems are average and a few are somewhat challenging.
Click HERE to see a detailed solution to problem 1.
Click HERE to see a detailed solution to problem 2.
Click HERE to see a detailed solution to problem 3.
Click HERE to see a detailed solution to problem 4.
Click HERE to see a detailed solution to problem 5.
Click HERE to see a detailed solution to problem 6.
Click HERE to see a detailed solution to problem 7.
Click HERE to see a detailed solution to problem 8.
Click HERE to see a detailed solution to problem 9.
Click HERE to see a detailed solution to problem 10.
Click HERE to see a detailed solution to problem 11.
Click HERE to see a detailed solution to problem 12.
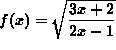 .
.
Click HERE to see a detailed solution to problem 13.
Click HERE to see a detailed solution to problem 14.
Click HERE to see a detailed solution to problem 15.
Click HERE to see a detailed solution to problem 16.
Click HERE to see a detailed solution to problem 17.
Click HERE to see a detailed solution to problem 18.
Click HERE to see a detailed solution to problem 19.
Your comments and suggestions are welcome. Please e-mail any correspondence to Duane Kouba by clicking on the following address :