SOLUTION 6: Draw a right triangle with dimensions $x, y,$ and $13$, and assume that $x$ and $y$ are functions of time $t$.
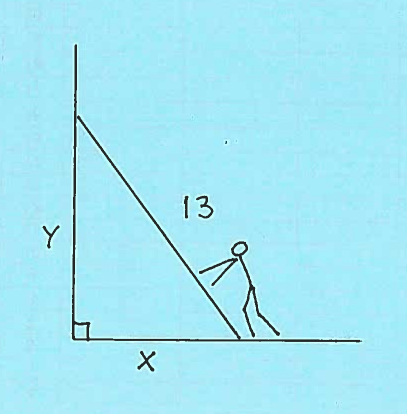
GIVEN: $ \ \ \ \displaystyle{ dx \over dt } = -2 \ in/min. $ (It is negative since $x$ is decreasing.)
FIND: $ \ \ \ \displaystyle{ dy \over dt } $ when $ \ \ \ a.) \ x = 5 \ ft. $ $ \ \ \ b.) \ x = 1 \ ft. $
Using the Pythagorean Theorem we get that
$$ x^2+y^2=13^2=169 $$
Now differentiate this length equation with respect to time $t $, getting
$$ D \{ x^2+y^2 \} = D \{ 169 \} \ \ \ \longrightarrow $$
$$ 2 x \displaystyle{ dx \over dt } + 2y \displaystyle{ dy \over dt } = 0 \ \ \ \longrightarrow $$
$$ (**) \ \ \ \ \ \ \ \ \ \ \ \ \ \ x \displaystyle{ dx \over dt } + y \displaystyle{ dy \over dt } = 0 \ \ \ \longrightarrow $$
$\Big($ a.) Now let $ \displaystyle{ dx \over dt } = -2 $ and $ x =5$ in equation (**). The Pythagorean Theorem equation becomes $ \ 5^2+y^2=169 \ \ \rightarrow \ y^2=144 \ \ \rightarrow \ y=12$ in equation (**). $ \Big) $
$$ (5)(-2)+ (12) \displaystyle{ dy \over dt } = 0 \ \ \ \longrightarrow $$
$$ 12 \displaystyle{ dy \over dt } = 10 \ \ \ \longrightarrow $$
$$ \displaystyle{ dy \over dt } = {10 \over 12} \ \ \ \longrightarrow $$
$$ \displaystyle{ dy \over dt } = { 5 \over 6} \ ft/sec. \approx 0.833 \ ft/sec. $$
$\Big($ b.) Now let $ \displaystyle{ dx \over dt } = -2 $ and $ x =1$ in equation (**). The Pythagorean Theorem equation becomes $ \ 1^2+y^2=169 \ \ \rightarrow \ y^2=168 \ \ \rightarrow \ y=\sqrt{168} $ in equation (**). $ \Big) $
$$ (1)(-2)+ (\sqrt{168}) \displaystyle{ dy \over dt } = 0 \ \ \ \longrightarrow $$
$$ \sqrt{168} \displaystyle{ dy \over dt } = 2 \ \ \ \longrightarrow $$
$$ \displaystyle{ dy \over dt } = { 2 \over \sqrt{168}} \ ft/sec. \approx 0.154 \ ft/sec. $$
Click HERE to return to the list of problems.

