SOLUTION 8: Draw a closed right circular cylinder of base radius $r$ and height $h$, and assume that $r$ and $h$ are functions of time $t$.
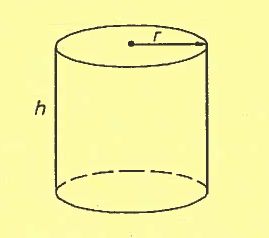
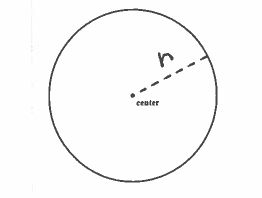
$ \ \ \ \ $ a.) The surface area of a closed right circular cylinder of radius $r$ is the sum of the areas of two circles and a rectangle:
$$ S= \pi r^2 + \pi r^2 + (base)(height) \ \ \ \ \longrightarrow $$
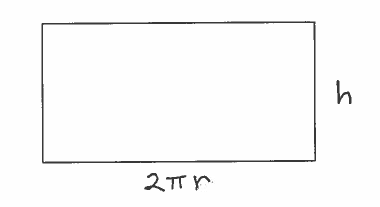
$$ S= 2\pi r^2 + (circumference \ of \ circle)(height) \ \ \ \ \longrightarrow $$
$$ S= 2\pi r^2 + (2\pi r)(h) \ \ \ \ \longrightarrow $$
$$ S= 2\pi r^2 + 2\pi r h $$

GIVEN: $ \ \ \ \displaystyle{ dr \over dt } = 5 \ cm/hr.$ and $ \displaystyle{ dh \over dt } = -4 \ cm/hr.$
FIND: $ \ \ \ \displaystyle{ dS \over dt } $ when $ r=20 \ cm. $ and $ h=12 \ cm. $
Now differentiate the surface area equation with respect to time $t $ using the product rule, getting
$$ D \{ S \} = D \{ 2\pi r^2 + 2\pi rh \} \ \ \ \longrightarrow $$
$$ \displaystyle{ dS \over dt } = 2 \pi \cdot 2r \displaystyle{ dr \over dt } + ( 2 \pi r \cdot \displaystyle{ dh \over dt } +
2 \pi \displaystyle{ dr \over dt } \cdot h ) \ \ \ \longrightarrow $$
$\Big($ Now let $ \displaystyle{ dr \over dt } = 5, \displaystyle{ dh \over dt } = -4, r=20,$ and $ h =12. \Big)$
$$ \displaystyle{ dS \over dt } = 4 \pi (20) (5) + 2 \pi (20)(-4) +
2 \pi (5) (12) \ \ \ \longrightarrow $$
$$ \displaystyle{ dS \over dt } = 400 \pi -160 \pi + 120 \pi \ \ \ \longrightarrow $$
$$ \displaystyle{ dS \over dt } = 360 \pi \ cm^2/hr. \approx 1130.97 \ cm^2/hr. $$
$ \ \ \ \ $ b.) The volume of a closed right circular cylinder of radius $r$ is
$$ V = (area \ of \ circular \ base)(height) \ \ \ \ \longrightarrow $$
$$ V = \pi r^2 h $$
GIVEN: $ \ \ \ \displaystyle{ dr \over dt } = 5 \ cm/hr.$ and $ \displaystyle{ dh \over dt } = -4 \ cm/hr.$
FIND: $ \ \ \ \displaystyle{ dV \over dt } $ when $ r=20 \ cm. $ and $ h=12 \ cm. $
Now differentiate the volume equation with respect to time $t$ using the product rule, getting
$$ D \{ V \} = D \{ \pi r^2 h \} \ \ \ \longrightarrow $$
$$ \displaystyle{ dV \over dt } = \pi r^2 \cdot \displaystyle{ dh \over dt } + 2\pi r \displaystyle{ dr \over dt } \cdot h \ \ \ \longrightarrow $$
$\Big($ Now let $ \displaystyle{ dr \over dt } = 5, \displaystyle{ dh \over dt } = -4, r=20,$ and $ h =12. \Big) $
$$ \displaystyle{ dV \over dt } = \pi (20)^2 (-4) + 2 \pi (20) (5)(12) \ \ \ \longrightarrow $$
$$ \displaystyle{ dV \over dt } = -1600 \pi + 2400 \pi \ \ \ \longrightarrow $$
$$ \displaystyle{ dV \over dt } = 800 \pi \ cm^3/hr. \approx 2513.27 \ cm^3/hr. $$
Click HERE to return to the list of problems.




