SOLUTION 9: Consider the given isosceles triangle of base $10$ and edges $x$, and assume that $x$ is a function of time $t$.

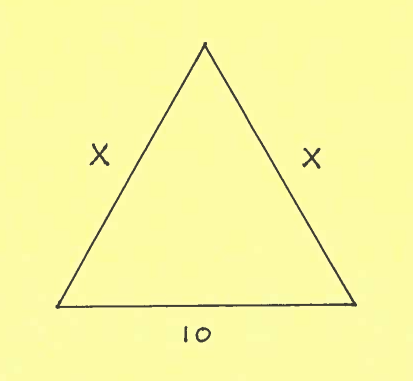
tex2html_wrap_inline125



$ \ \ \ \ $ a.) The perimeter of the triangle is $$ P= x+x+10 \ \ \ \ \longrightarrow $$ $$ P= 2x+10 $$ GIVEN: $ \ \ \ \displaystyle{ dx \over dt } = 4 \ in/min.$

FIND: $ \ \ \ \displaystyle{ dP \over dt } $ when $ x=13 \ in. $

Now differentiate the perimeter equation with respect to time $t $, getting

$$ D \{ P \} = D \{ 2x+10 \} \ \ \ \longrightarrow $$ $$ \displaystyle{ dP \over dt } = 2 \displaystyle{ dx \over dt } \ \ \ \longrightarrow $$

$\Big($ Now let $ \displaystyle{ dx \over dt } = 4. \Big) $

$$ \displaystyle{ dP \over dt } = 2 (4) \ \ \ \longrightarrow $$ $$ \displaystyle{ dP \over dt } = 8 \ in^2/min. $$

$ \ \ \ \ $ b.) Consider the given isosceles triangle of base $10$, edges $x$, and height $h$, and assume that $x$ and $h$ are functions of time $t$. Divide the triangle into two right triangles of height $h$.

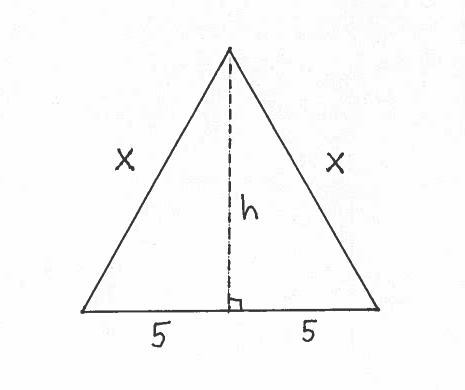
tex2html_wrap_inline125



Using the Pythagorean Theorem we get the following height equation: $$ 5^2+h^2=x^2 \ \ \ \longrightarrow $$ $$ h^2=x^2 - 25 $$ GIVEN: $ \ \ \ \displaystyle{ dx \over dt } = 4 \ in/min.$

FIND: $ \ \ \ \displaystyle{ dh \over dt } $ when $ x=13 \ in. $

Now differentiate the height equation with respect to time $t$, getting

$$ D \{ h^2 \} = D \{ x^2 - 25 \} \ \ \ \ \longrightarrow $$ $$ 2h \displaystyle{ dh \over dt } = 2x \displaystyle{ dx \over dt } \ \ \ \ \longrightarrow $$

$ \Big($ Multiply both sides of the equation by $ 1/2 . \Big)$

$$ h \displaystyle{ dh \over dt } = x \displaystyle{ dx \over dt } \ \ \ \ \longrightarrow $$



$\Big($ Let $ \ x=13 \ $ in the height equation $ \ 25+h^2=x^2 \ ,$ getting $ \ 25 + h^2 = 13^2=169 \ \ \rightarrow \ \ \ h^2=144 \ \ \rightarrow \ h=12 . $ Now let $ \displaystyle{ dx \over dt } = 4, x=13,$ and $ h =12. \Big)$

$$ (12) \displaystyle{ dh \over dt } = (13)(4) \ \ \ \longrightarrow $$ $$ \displaystyle{ dh \over dt } = {52 \over 12 } \ \ \ \longrightarrow $$ $$ \displaystyle{ dh \over dt } = { 13 \over 3 } \ in/min. $$

$ \ \ \ \ $ c.) Consider the given isosceles triangle of base $10$, edges $x$, and height $h$, and assume that $x$ and $h$ are functions of time $t$. The area of the isosceles triangle is $$ A= (1/2)(base)(height) \ \ \ \ \longrightarrow $$ $$ A= (1/2)(10)h \ \ \ \ \longrightarrow $$ $$ A= 5h \ \ \ \ \longrightarrow $$

tex2html_wrap_inline125

GIVEN: $ \ \ \ \displaystyle{ dx \over dt } = 4 \ in/min.$

FIND: $ \ \ \ \displaystyle{ dA \over dt } $ when $ x=13 \ in. $

Now differentiate the area equation with respect to time $t$, getting

$$ D \{ A \} = D \{ 5h \} \ \ \ \longrightarrow $$ $$ \displaystyle{ dA \over dt } = 5 \displaystyle{ dh \over dt } \ \ \ \ \longrightarrow $$

$\Big($ See the solution to solution 9 part b. and let $ \displaystyle{ dh \over dt } = { 13 \over 3 }. \Big) $

$$ \displaystyle{ dA \over dt } = 5 \Big({ 13 \over 3 }\Big) \ \ \ \ \longrightarrow $$ $$ \displaystyle{ dV \over dt } = { 65 \over 3 } \ in^2/min. $$

Click HERE to return to the list of problems.