SOLUTION 10: Consider the given closed rectangular box with dimensions $x, y,$ and $z$, and assume that $x, y,$ and $z$ are functions of time $t$.
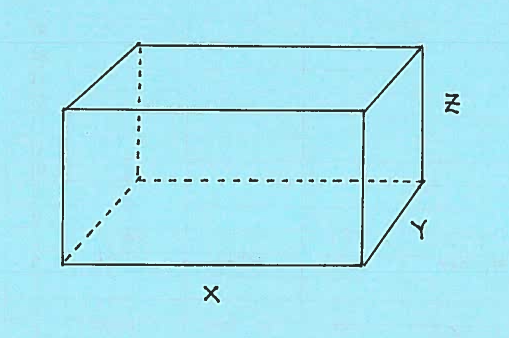
$ \ \ \ \ $ a.) The surface area of the box (Add the areas of six rectangular surfaces.) is
$$ S= xy+xy+xz+xz+yz+yz \ \ \ \ \longrightarrow $$
$$ S= 2xy+2xz+2yz $$
GIVEN: $ \ \ \ \displaystyle{ dx \over dt } = 4 \ ft/hr.$, $\displaystyle{ dy \over dt } = -6 \ ft/hr.$, and $\displaystyle{ dz \over dt } = 3 \ ft/hr.$
FIND: $ \ \ \ \displaystyle{ dS \over dt } $ when $ x=5 \ ft. $, $ y=4 \ ft. $, and $ z=6 \ ft. $
Now differentiate the surface area equation with respect to time $t $ using the product rule, getting
$$ D \{ S \} = D \{ 2xy + 2xz + 2yz \} \ \ \ \longrightarrow $$
$$ \displaystyle{ dS \over dt } = 2 ( x \displaystyle{ dy \over dt } + \displaystyle{ dx \over dt } y )
+ 2 ( x \displaystyle{ dz \over dt } + \displaystyle{ dx \over dt } z ) + 2 ( y \displaystyle{ dz \over dt } + \displaystyle{ dy \over dt } z ) \ \ \ \longrightarrow $$
$\Big($ Now let $ \displaystyle{ dx \over dt } = 4, \displaystyle{ dy \over dt } = -6, \displaystyle{ dz \over dt } = 3, x=5, y=4$, and $z=6. \Big) $
$$ \displaystyle{ dS \over dt } = 2 ( (5)(-6) + (4)(4) )
+ 2 ( (5)(3) + (4) (6) ) + 2 ( (4)(3) + (-6) (6) )
\ \ \ \longrightarrow $$
$$ \displaystyle{ dS \over dt } = 2 ( -14 ) + 2 ( 39 ) + 2 ( -24 ) \ \ \ \longrightarrow $$
$$ \displaystyle{ dS \over dt } = -28 + 78 + -48 \ \ \ \longrightarrow $$
$$ \displaystyle{ dS \over dt } = 2 \ ft^2/min. $$
$ \ \ \ \ $ b.) The volume of the box is
$$ V= (length)(width)(height) \ \ \ \ \longrightarrow $$
$$ V=xyz $$
GIVEN: $ \ \ \ \displaystyle{ dx \over dt } = 4 \ ft/hr.$, $\displaystyle{ dy \over dt } = -6 \ ft/hr.$, and $\displaystyle{ dz \over dt } = 3 \ ft/hr.$
FIND: $ \ \ \ \displaystyle{ dV \over dt } $ when $ x=5 \ ft. $, $ y=4 \ ft. $, and $ z=6 \ ft. $
Now differentiate the volume equation with respect to time $t $ using the triple product rule, getting
$$ D \{ V \} = D \{ xyz \} \ \ \ \longrightarrow $$
$$ \displaystyle{ dV \over dt } = \displaystyle{ dx \over dt }yz + x \displaystyle{ dy \over dt }z + xy\displaystyle{ dz \over dt } \ \ \ \longrightarrow $$
$\Big($ Now let $ \displaystyle{ dx \over dt } = 4, \displaystyle{ dy \over dt } = -6, \displaystyle{ dz \over dt } = 3, x=5, y=4$, and $z=6. \Big) $
$$ \displaystyle{ dV \over dt } = (4)(4)(6) + (5)(-6)(6) + (5)(4)(3) \ \ \ \ \longrightarrow $$
$$ \displaystyle{ dV \over dt } = 96-180+60 \ \ \ \ \longrightarrow $$
$$ \displaystyle{ dV \over dt } = -24 \ ft^3/hr. $$
$ \ \ \ \ $ c.) Consider the given closed rectangular box with dimensions $x$ feet by $y$ feet by $z$ feet, and the main diagonal of length $L$ feet in the given diagram.
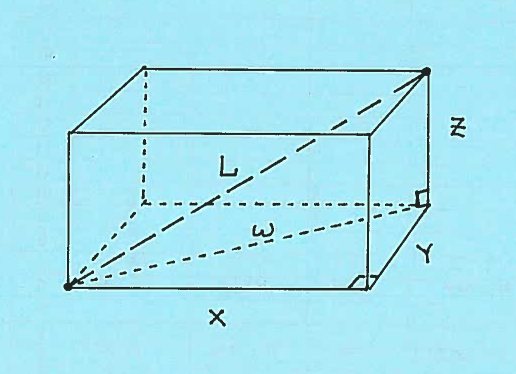
Consider the two right triangles of edge lengths $x, y,$ and $w$ and $w, z,$ and $L$, resp. Apply the Pythagorean Theorem to each right triangle getting
$$ x^2+y^2=w^2 \ \ \ and \ \ \ w^2 + z^2 = L^2 $$
Substituting for $w^2$ leads to the following main diagonal equation:
$$ L^2 = x^2+y^2 + z^2 $$
GIVEN: $ \ \ \ \displaystyle{ dx \over dt } = 4 \ ft/hr.$, $\displaystyle{ dy \over dt } = -6 \ ft/hr.$, and $\displaystyle{ dz \over dt } = 3 \ ft/hr.$
FIND: $ \ \ \ \displaystyle{ dS \over dt } $ when $ x=5 \ ft. $, $ y=4 \ ft. $, and $ z=6 \ ft. $
Now differentiate the main diagonal equation with respect to time $t$, getting
$$ D \{ L^2 \} = D \{ x^2+y^2 + z^2 \} \ \ \ \longrightarrow $$
$$ 2L \displaystyle{ dL \over dt } = 2x \displaystyle{ dx \over dt } + 2y \displaystyle{ dy \over dt } + 2z \displaystyle{ dz \over dt } \ \ \ \longrightarrow $$
$$ L \displaystyle{ dL \over dt } = x \displaystyle{ dx \over dt } + y \displaystyle{ dy \over dt } + z \displaystyle{ dz \over dt } \ \ \ \longrightarrow $$
$\Big($ Now let $ \displaystyle{ dx \over dt } = 4, \displaystyle{ dy \over dt } = -6, \displaystyle{ dz \over dt } = 3, x=5, y=4$, and $z=6 .$ The equation $ L^2 = x^2+y^2+z^2$ becomes $ L^2=5^2+4^2+6^2 $, so that $ L^2=77 $ and $L=\sqrt{77}. \Big) $
$$ \sqrt{77} \displaystyle{ dL \over dt } = (5)(4) + (4)(-6) + (6) (3) \ \ \ \ \longrightarrow $$
$$ \sqrt{77} \displaystyle{ dL \over dt } = 14 \ \ \ \ \longrightarrow $$
$$ \displaystyle{ dL \over dt } = { 14 \over \sqrt{77} } \ ft/hr. \approx 1.595 ft/hr. $$
Click HERE to return to the list of problems.


