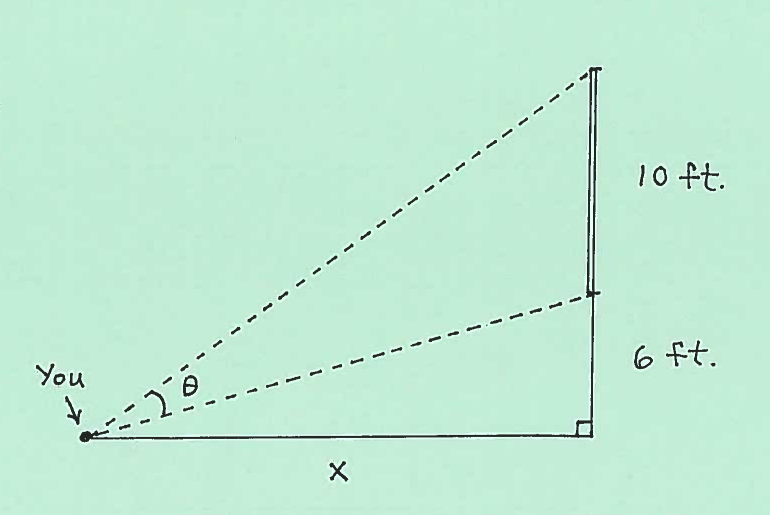
SOLUTION 14: Consider the given right triangle with legs of length $x \ cm.$ and $y \ cm.$ and angle $ \theta $ radians, and assume that $ x, y,$ and $ \theta $ are functions of time $t$.
a.) Label angle $ \alpha $ radians in the right triangle with legs of length $x$ and $6$ feet.
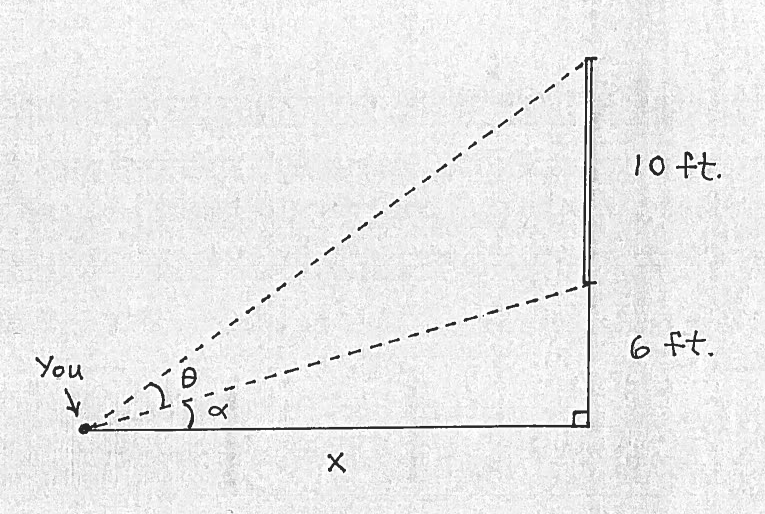
Using trigonometry we can say that
$$ \tan \alpha = \displaystyle{ opposite \over adjacent } = { 6 \over x } \ \ \ \longrightarrow $$
$$ \alpha = \arctan \Big({ 6 \over x } \Big) $$
and
$$ \tan ( \theta +\alpha) = \displaystyle{ opposite \over adjacent } = { 10+6 \over x } \ \ \ \longrightarrow $$
$$ \theta + \alpha = \arctan \Big({ 16 \over x } \Big) \ \ \ \longrightarrow $$
$$ \theta = \arctan \Big({ 16 \over x } \Big) - \alpha \ \ \ \longrightarrow $$
$$ \theta = \arctan \Big({ 16 \over x } \Big) - \arctan \Big({ 6 \over x } \Big) $$
b.) Begin with the $ \theta $ equation from part a.
GIVEN: $ \ \ \ \displaystyle{ dx \over dt } = 10 \ ft/min. $
FIND: $ \ \ \ \displaystyle{ d \theta \over dt } $ when $ \ \ $ i.) $ \ x =8 \ ft. $ $ \ \ $ ii.) $ \ x = 20 \ ft. $
Recall that $ D \{ \arctan f(x) \} = \displaystyle{ 1 \over 1 + (f(x))^2 } \cdot f'(x). $ Now differentiate the theta equation with respect to time $t $ getting
$$ D \{ \theta \} = D \{ \arctan \Big({ 16 \over x } \Big) \} - D \{ \arctan \Big({ 6 \over x } \Big) \} \ \ \ \longrightarrow $$
$$ \displaystyle{ d \theta \over dt } = \displaystyle{ 1 \over 1 + (16/x)^2 } \cdot D\Big\{ {16 \over x} \Big\}
- \displaystyle{ 1 \over 1 + (6/x)^2 } \cdot D\Big\{ {6 \over x} \Big\} \ \ \ \longrightarrow $$
$$ \displaystyle{ d \theta \over dt } = \displaystyle{ 1 \over 1 + { 256 \over x^2 } } \cdot \Big\{ {-16 \over x^2} \Big\} \cdot \displaystyle{ dx \over dt }
- \displaystyle{ 1 \over 1 + { 36 \over x^2 } } \cdot \Big\{ {-6 \over x^2} \Big\} \cdot \displaystyle{ dx \over dt } \ \ \ \longrightarrow $$
$$ \displaystyle{ d \theta \over dt } = \displaystyle{ -16 \over x^2 + 256 } \cdot \displaystyle{ dx \over dt }
- \displaystyle{ -6 \over x^2 + 36 } \cdot \displaystyle{ dx \over dt } \ \ \ \longrightarrow $$
$$ (**) \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \displaystyle{ d \theta \over dt } = \displaystyle{ 6 \over x^2 + 36 } \cdot \displaystyle{ dx \over dt } - \displaystyle{ 16 \over x^2 + 256 } \cdot \displaystyle{ dx \over dt }
\ \ \ \longrightarrow $$
$\Big($ i. Now let $ \displaystyle{ dx \over dt } = 10 $ and $ \ x=8 $ in equation (**). $\Big)$
$$ \displaystyle{ d \theta \over dt } = \displaystyle{ 6 \over 8^2 + 36 } (10) - \displaystyle{ 16 \over 8^2 + 256 } (10)
\ \ \ \longrightarrow $$
$$ \displaystyle{ d \theta \over dt } = \displaystyle{ 60 \over 100 } - \displaystyle{ 160 \over 320 } = { 3 \over 5 } - { 1 \over 2 } = {1 \over 10 } = 0.100 \ radians/min. $$
$\Big($ ii. Now let $ \displaystyle{ dx \over dt } = 10 $ and $ \ x=20 $ in equation (**). $\Big)$
$$ \displaystyle{ d \theta \over dt } = \displaystyle{ 6 \over 20^2 + 36 } \cdot (20) - \displaystyle{ 16 \over 20^2 + 256 } \cdot (20)
\ \ \ \longrightarrow $$
$$ \displaystyle{ d \theta \over dt } = \displaystyle{ 120 \over 436 } - \displaystyle{ 320 \over 656 } = { 30 \over 109 } - { 20 \over 41 } = {-950 \over 4469 } \approx -0.213 \ radians/min. $$
Click HERE to return to the list of problems.


