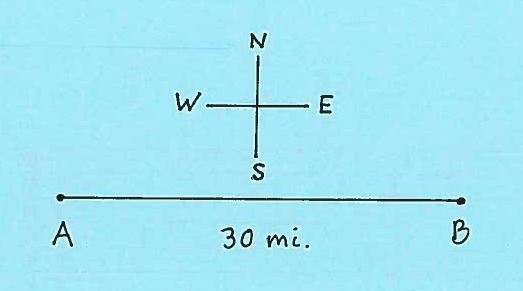
SOLUTION 16: Car B starts 30 miles directly east of car A.
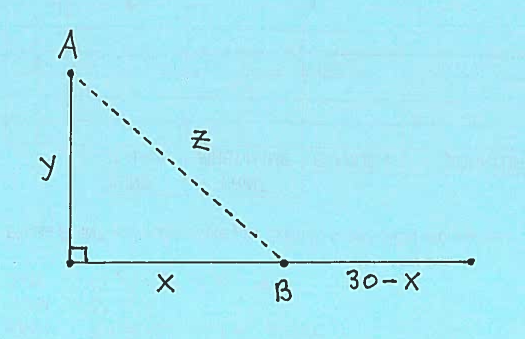
Here is a diagram showing the positions of cars A and B after $t $ hours. Assume that distances $x, y,$ and $z$
are all functions of time $t$.
GIVEN: $ \ \ \ \displaystyle{ dx \over dt } = -90 \ mph $ (It is negative since $x$ is decreasing.) and $ \displaystyle{ dy \over dt } = 60 \ mph $.
FIND: $ \ \ \ \displaystyle{ dz \over dt } $ when $ \ \ $ a.) $ \ t=1/5 \ hr. $ $ \ \ $ b.) $ \ t=1/3 \ hr. $
Using the Pythagorean Theorem we get the following distance equation:
$$ x^2+y^2=z^2 $$
Differentiating the distance equation, we get
$$ D \{ x^2+y^2 \} = \{ z^2 \} \ \ \ \ \longrightarrow $$
$$ 2x \displaystyle{ dx \over dt } + 2y \displaystyle{ dy \over dt } = 2 z \displaystyle{ dz \over dt } \ \ \ \ \longrightarrow $$
$\Big( $ Multiply both sides of the equation by $ \displaystyle{ 1 \over 2 }. \Big)$
$$ (**) \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ x \displaystyle{ dx \over dt } + y \displaystyle{ dy \over dt } = z \displaystyle{ dz \over dt } \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ $$
Recall that:
$$ (Distance) = (Constant \ Rate)(Time) $$
$ \ \ \ \ \ $ a.) If $t=1/5 \ hr.$, then car B has traveled west $ (90 \ mph)(1/5 \ hr.) = 18 \ miles, $ so that $ x=30-18=12 \ miles $; and car A has traveled north $ (60 \ mph)(1/5 \ hr.) = 12 \ miles, $ so that $y=12 \ miles.$ Using the distance equation we get that $ \ (12)^2+(12)^2= z^2 \ \ \rightarrow \ z^2= 288 \ \ \rightarrow \ z = \sqrt{288} \approx 16.97 \ miles. $
Now let $ \displaystyle{ dx \over dt } = -90, \displaystyle{ dy \over dt } = 60, x=12, y=12 $ and $ \ z=\sqrt{288} $ in equation (**), getting
$$ (12)(-90) + (12)(60) = (\sqrt{288}) \displaystyle{ dz \over dt } \ \ \ \ \longrightarrow $$
$$ -1080 + 720 = \sqrt{288} \displaystyle{ dz \over dt } \ \ \ \ \longrightarrow $$
$$ \displaystyle{ dz \over dt } = { -360 \over \sqrt{288} } \approx -21.21 \ mph $$
$ \ \ \ \ \ $ b.) If $t=1/3 \ hr.$, then car B has traveled west $ (90 \ mph)(1/3 \ hr.) = 30 \ miles, $ so that $ x=30-30=0 \ miles $; and car A has traveled north $ (60 \ mph)(1/3 \ hr.) = 20 \ miles, $ so that $y=20 \ miles.$ Using the distance equation we get that $ \ (0)^2+(20)^2= z^2 \ \ \ \rightarrow \ z^2= 400 \ \ \ \rightarrow \ z = 20 \ miles. $
Now let $ \displaystyle{ dx \over dt } = -90, \displaystyle{ dy \over dt } = 45, x=0, y=20 $ and $ \ z=20 $ in equation (**), getting
$$ (0)(-90) + (20)(60) = (20) \displaystyle{ dz \over dt } \ \ \ \ \longrightarrow $$
$$ 1200 = 20 \displaystyle{ dz \over dt } \ \ \ \ \longrightarrow $$
$$ \displaystyle{ dz \over dt } = 60 \ mph $$
Click HERE to return to the list of problems.


