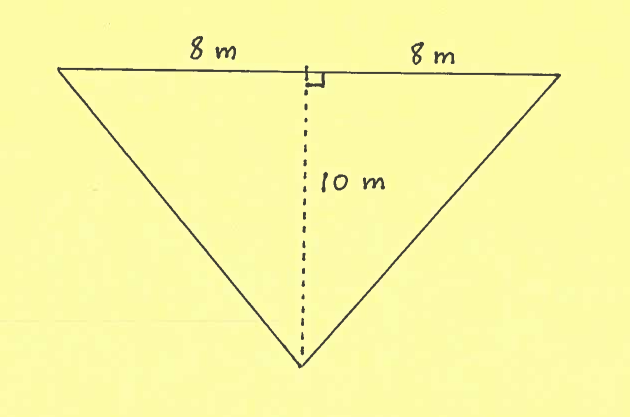
SOLUTION 16: Consider the given side view of the conical tank of height $ 10$ meters and base radius $8$ meters.
Consider the cone of water of depth $h$ meters and the right triangle with legs $r$ and $h$ in the side view of the conical tank. Assume that lengths $r$ and $h$ are both functions of time $t$.
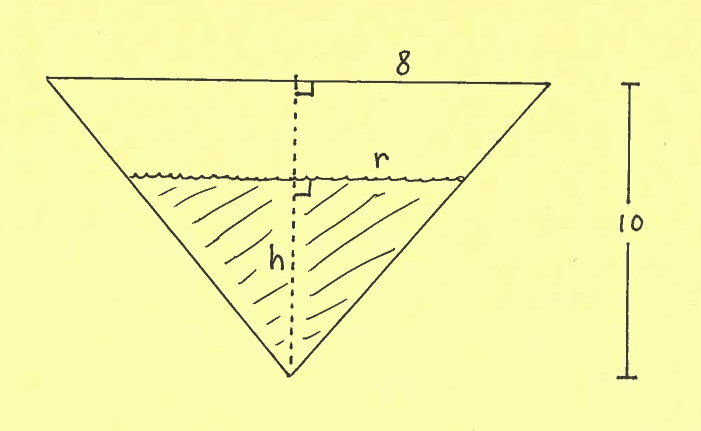
RECALL: The volume of a right circular cone of height $h$ and base radius $r$ is
$$ V = \displaystyle{ 1 \over 3 } \pi r^2 h $$
GIVEN: $ \ \ \ \displaystyle{ dV\over dt } = \pi \ m^3/min. $
FIND: $ \ \ \ \displaystyle{ dh \over dt } $ when $ \ \ $ a.) $ \ h=1 \ m. $ $ \ \ $ b.) $ \ h=9 \ m. $
First consider the two given similar right triangles. Use them to write $r$ in terms of $h$.
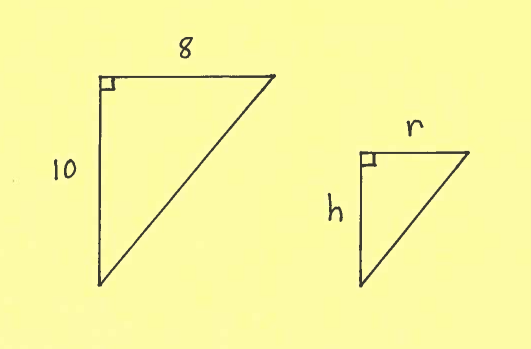
Using similar triangles we can conclude that
$$ \displaystyle{ r \over h } = { 8 \over 10 } \ \ \ \ \longrightarrow $$
$$ \displaystyle{ r \over h } = { 4 \over 5 } \ \ \ \ \longrightarrow $$
$$ r = \displaystyle{ 4 \over 5 }h $$
The volume equation can now be rewritten as
$$ V = \displaystyle{ 1 \over 3 } \pi \Big\{ { 4 \over 5 }h \Big\}^2 h \ \ \ \ \longrightarrow $$
$$ V = \displaystyle{ 16 \over 75 } \pi h^3 $$
Differentiating the volume equation, we get
$$ D \{ V \} = D\{ \displaystyle{ 16 \over 75 } \pi h^3 \} \ \ \ \ \longrightarrow $$
$$ \displaystyle{ dV \over dt } = \displaystyle{ 16 \over 75 } \pi \cdot 3h^2 { dh \over dt } \ \ \ \ \longrightarrow $$
$$ (**) \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \displaystyle{ dV \over dt } = \displaystyle{ 16 \over 25 } \pi h^2 { dh \over dt } \ \ \ \ \longrightarrow $$
$\Big($ a.) Now let $ \displaystyle{ dV \over dt } = \pi $ and $ \ h=1 . \Big) $
$$ \pi = \displaystyle{ 16 \over 25 } \pi (1)^2 { dh \over dt } \ \ \ \ \longrightarrow $$
$\Big($Divide both sides of the equation by $ \pi. \Big)$
$$ 1 = \displaystyle{ 16 \over 25 } { dh \over dt } \ \ \ \ \longrightarrow $$
$$ \displaystyle{ dh \over dt } = { 25 \over 16 } =1.5625 \ meters/min. $$
$\Big($ b.) Now let $ \displaystyle{ dV \over dt } = \pi $ and $ \ h=9 $ in equation (**). $\Big)$
$$ \pi = \displaystyle{ 16 \over 25 } \pi (9)^2 { dh \over dt } \ \ \ \ \longrightarrow $$
$$ 1 = \displaystyle{ 16 \over 25 } (81) { dh \over dt } \ \ \ \ \longrightarrow $$
$$ 1 = \displaystyle{ 1296 \over 25 } { dh \over dt } \ \ \ \ \longrightarrow $$
$$ \displaystyle{ dh \over dt } = { 25 \over 1296 } \approx 0.019 \ meters/min. $$
Click HERE to return to the list of problems.



