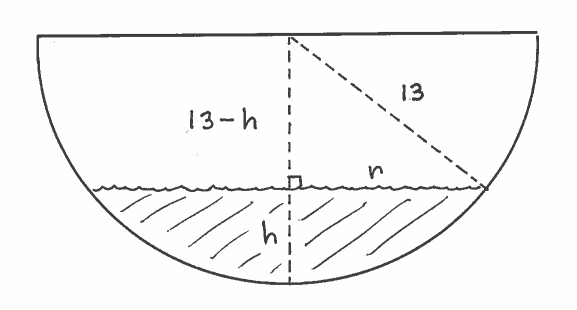
SOLUTION 17: Consider the given side view of the open hemisperical tank of radius 13 feet filled with oil to a depth of $ h$ feet. Assume that the circular surface area of the oil has radius $r$ feet, and assume that $r$ and $h$ are both functions of time $t$.
GIVEN: $ \ \ \ \displaystyle{ dh \over dt } = 3 \ ft/min. $
FIND: $ \ \ \ \displaystyle{ dh \over dt } $ when $ \ \ $ a.) $ \ h=1 \ ft. $ $ \ \ $ b.) $ \ h=8 \ ft. $
Applying the Pythagorean Theorem to the given right triangle in the side view diagram, we get
$$ r^2 + (13-h)^2 = 13^2 \ \ \ \ \longrightarrow $$
$$ r^2 + 169 - 26h + h^2 = 169 \ \ \ \ \longrightarrow $$
$$ r^2 = 26h - h^2 $$
Differentiating this radius equation, we get
$$ D \{ r^2 \} = D \{ \displaystyle{ 26h-h^2 } \} \ \ \ \ \longrightarrow $$
$$ 2r \displaystyle{ dr \over dt } = 26 \displaystyle{ dh \over dt } - 2h { dh \over dt } \ \ \ \ \longrightarrow $$
$\Big($Multiply both sides of the equation by $ \displaystyle{ 1 \over 2 }. \Big)$
$$ (**) \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ r \displaystyle{ dr \over dt } = 13 \displaystyle{ dh \over dt } - h { dh \over dt } \ \ \ \ \longrightarrow $$
$\Big($ a.) Now let $ \displaystyle{ dh \over dt } = 3 $ and $ \ h=1 $ in equation (**). If $h=1$ in the right triangle, then
$ \ r^2+12^2=13^2 \ \rightarrow \ r^2+144=169 \ \rightarrow \ r^2=25 \ \rightarrow r=5. \Big)$
$$ (5) \displaystyle{ dr \over dt } = 13 (3) - (1) (3) \ \ \ \ \longrightarrow $$
$$ 5 \displaystyle{ dr \over dt } = 36 \ \ \ \ \longrightarrow $$
$$ \displaystyle{ dr \over dt } = { 36 \over 5 } = 7.2 \ ft/min. $$
$\Big($ b.) Now let $ \displaystyle{ dh \over dt } = 3 $ and $ \ h=8 $ in equation (**). If $h=8$ in the right triangle, then
$ \ r^2+5^2=13^2 \ \rightarrow \ r^2+25=169 \ \rightarrow \ r^2=144 \ \rightarrow r=12. \Big) $
$$ (12) \displaystyle{ dr \over dt } = 13 (3) - (8) (3) \ \ \ \ \longrightarrow $$
$$ 12 \displaystyle{ dr \over dt } = 15 \ \ \ \ \longrightarrow $$
$$ \displaystyle{ dr \over dt } = { 15 \over 12 } = 1.25 \ ft/min. $$
Click HERE to return to the list of problems.



