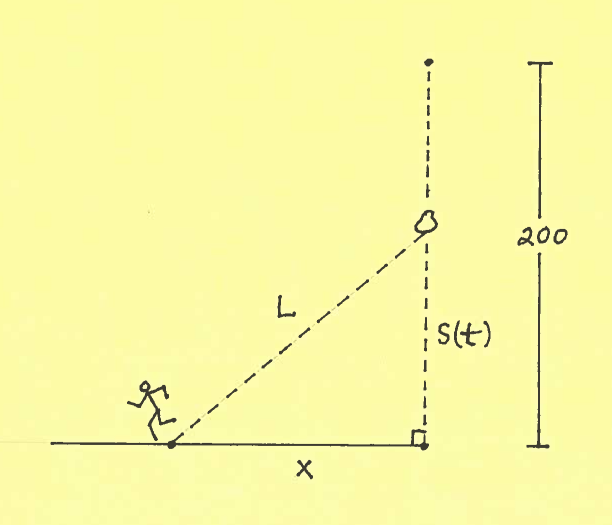
SOLUTION 19: Consider the given diagram where $s(t)$ feet is the height of the boulder above the ground after falling for $t$ seconds and $L$ is the distance between the running you and the falling boulder. Assume that $x, L,$ and $s(t)$ are all functions of time $t$.
GIVEN: $ \ \ \ \displaystyle{ dx \over dt } = 10 \ ft/sec. $
FIND: $ \ \ \ \displaystyle{ dL \over dt } $ when $ \ \ $ a.) $ \ t=1 \ sec. $ $ \ \ $ b.) $ \ t=3 \ sec. $
Recall from elementary physics that the height $s(t)$ in feet of a falling object under the influence of only gravity is
$$ s(t) = -16t^2+ v_{o} t + s_{o}$$
where $ s_{o} $ is the initial height and $ v_{o} $ is the initial velocity of the falling object. For this problem $ s_{o}=200 $ is the initial height and $ v_{o}=0 $ is the initial velocity, so that
$$ s(t) = -16t^2 + 200 $$
Using the Pythagorean Theorem, we now get that
$$ L^2 = x^2+ \{ s(t) \}^2 \ \ \ \ \longrightarrow $$
$$ L^2 = x^2+ ( -16t^2+200 )^2 $$
Differentiating this distance equation, we get
$$ D \{ L^2 \} = D \{ x^2 + ( -16t^2+200 )^2 \} \ \ \ \ \longrightarrow $$
$$ 2L \displaystyle{ dL \over dt } = 2x \displaystyle{ dx \over dt } + 2( -16t^2+200) \cdot (-32t) \ \ \ \ \longrightarrow $$
$\Big($Multiply both sides of the equation by $ \displaystyle{ 1 \over 2 }.\Big) $
$$ L \displaystyle{ dL \over dt } = x \displaystyle{ dx \over dt }
-32t ( -16t^2+200) \ \ \ \ \longrightarrow $$
$$ (**) \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ L \displaystyle{ dL \over dt } = x \displaystyle{ dx \over dt }
+ 512t^3-6400t \ \ \ \ \longrightarrow $$
$\Big($ a.) Now let $ \displaystyle{ dx \over dt } = 10 $ and $ \ t=1 $ in equation (**). Since you initially start at $x=12 $, the distance $ x $ feet after $t$ seconds is $ x=10t+12 $, so that $ x=10(1)+12=22 $ in equation (**). Since $ s(1)=-16(1)^2+200=184 $, it follows from the distance equation that $ \ L^2=22^2+184^2 \ \rightarrow L^2=34,340 \ \rightarrow L=\sqrt{34,340} \approx 185.31 $ in equation (**). $\Big)$
$$ ( \sqrt{34,340}) \displaystyle{ dL \over dt } = (22)(10) + 512 (1)^3- 6400(1) \ \ \ \ \longrightarrow $$
$$ \sqrt{34,340} \displaystyle{ dL \over dt } = -5668 \ \ \ \ \longrightarrow $$
$$ \displaystyle{ dL \over dt } = { -5668 \over \sqrt{34,340} } \approx -30.586 \ ft/sec. $$
$\Big($ b.) Now let $ \displaystyle{ dx \over dt } = 10 $ and $ \ t=3 $ in equation (**). Since you initially start at $x=12 $, the distance $ x $ feet after $t$ seconds is $ x=10t+12 $, so that $ x=10(3)+12=42 $ in equation (**). Since $ s(3)=-16(3)^2+200=56 $, it follows from the distance equation that $ \ L^2=42^2+56^2 \ \rightarrow \ L^2=4900 \ \rightarrow \ L=\sqrt{4900} = 70 $ in equation (**). $\Big)$
$$ (70) \displaystyle{ dL \over dt } = (42)(10) + 512 (3)^3 - 6400 (3) \ \ \ \ \longrightarrow $$
$$ 70 \displaystyle{ dL \over dt } = -4956 \ \ \ \ \longrightarrow $$
$$ \displaystyle{ dL \over dt } = { -4956 \over 70 } = -70.8 \ ft/sec. $$
Click HERE to return to the list of problems.

