SOLUTION 1 : First note that
![]()
because of the well-known properties of the sine function. Since we are computing the limit as x goes to infinity, it is reasonable to assume that x > 0 . Thus,
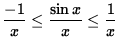 .
.
Since
![]() ,
,
it follows from the Squeeze Principle that
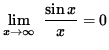 .
.
Click HERE to return to the list of problems.
SOLUTION 2 : First note that
![]()
because of the well-known properties of the cosine function. Now multiply by -1, reversing the inequalities and getting
![]()
or
![]() .
.
Next, add 2 to each component to get
![]() .
.
Since we are computing the limit as x goes to infinity, it is reasonable to assume that x + 3 > 0. Thus,
![]() .
.
Since
![]() ,
,
it follows from the Squeeze Principle that
![]() .
.
Click HERE to return to the list of problems.
SOLUTION 3 : First note that
![]()
because of the well-known properties of the cosine function, and therefore
![]() .
.
Since we are computing the limit as x goes to infinity, it is reasonable to assume that 3 - 2x < 0. Now divide each component by 3 - 2x, reversing the inequalities and getting
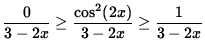 ,
,
or
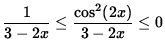 .
.
Since
![]() ,
,
it follows from the Squeeze Principle that
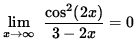 .
.
Click HERE to return to the list of problems.
SOLUTION 4 : Note that
![]() DOES NOT EXIST since values of
DOES NOT EXIST since values of
![]() oscillate between -1 and +1 as x approaches 0 from the left. However, this does NOT necessarily mean that
oscillate between -1 and +1 as x approaches 0 from the left. However, this does NOT necessarily mean that
![]() does not exist ! ? #. Indeed, x3 < 0 and
does not exist ! ? #. Indeed, x3 < 0 and
![]()
for x < 0. Multiply each component by x3, reversing the inequalities and getting
![]()
or
![]() .
.
Since
![]() ,
,
it follows from the Squeeze Principle that
![]() .
.
Click HERE to return to the list of problems.
SOLUTION 5 : First note that
![]() ,
,
so that
![]()
and
![]() .
.
Since we are computing the limit as x goes to infinity, it is reasonable to assume that x+100 > 0. Thus, dividing by x+100 and multiplying by x2, we get
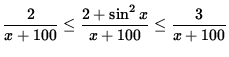
and
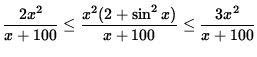 .
.
Then
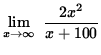 =
=
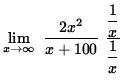
=
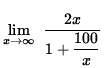
=
![]()
= ![]() .
.
Similarly,
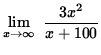 =
= ![]() .
.
Thus, it follows from the Squeeze Principle that
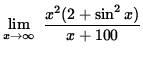 =
= ![]() (does not exist).
(does not exist).
Click HERE to return to the list of problems.
SOLUTION 6 : First note that
![]() ,
,
so that
![]() ,
,
![]() ,
,
and
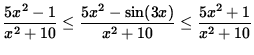 .
.
Then
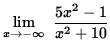
=
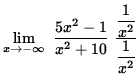
=
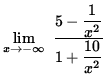
=
![]()
= 5 .
Similarly,
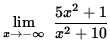 = 5 .
= 5 .
Thus, it follows from the Squeeze Principle that
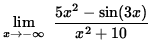 = 5 .
= 5 .
Click HERE to return to the list of problems.
SOLUTION 7 : First note that
![]()
and
![]() ,
,
so that
![]()
and
![]() .
.
Since we are computing the limit as x goes to negative infinity, it is reasonable to assume that x-3 < 0. Thus, dividing by x-3, we get
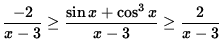
or
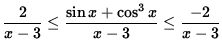 .
.
Now divide by x2 + 1 and multiply by x2 , getting
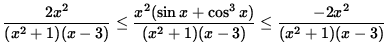 .
.
Then
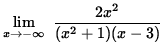
=
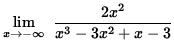
=
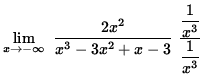
=
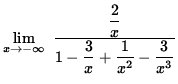
=
![]()
= 0 .
Similarly,
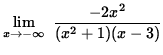 = 0 .
= 0 .
It follows from the Squeeze Principle that
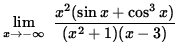 = 0 .
= 0 .
Click HERE to return to the list of problems.
SOLUTION 8 : Since
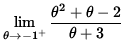 =
=
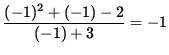
and
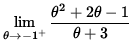 =
=
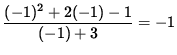 ,
,
it follows from the Squeeze Principle that
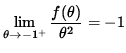 ,
,
that is,
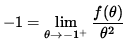
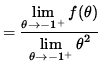
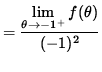
![]() .
.
Thus,
![]() .
.
Click HERE to return to the list of problems.
SOLUTION 9 : a.) First note that (See diagram below.)
area of triangle OAD < area of sector OAC < area of triangle OBC .
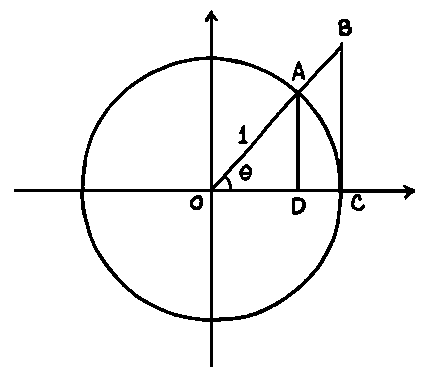
The area of triangle OAD is
![]() (base) (height)
(base) (height)
![]() .
.
The area of sector OAC is
![]() (area of circle)
(area of circle)
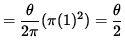 .
.
The area of triangle OBC is
![]() (base) (height)
(base) (height)
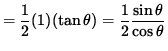 .
.
It follows that
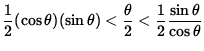
or
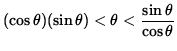 .
.
b.) If
![]() ,
then
,
then
![]() and
and
![]() , so that dividing by
, so that dividing by
![]() results in
results in
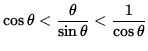 .
.
Taking reciprocals of these positive quantities gives
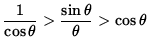
or
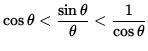 .
.
Since
![]() ,
,
it follows from the Squeeze Principle that
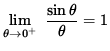 .
.
Click HERE to return to the list of problems.
SOLUTION 10 : Recall that function f is continuous at x=0 if
i.) f(0) is defined ,
ii.)
![]() exists ,
exists ,
and
iii.)
![]() .
.
First note that it is given that
i.) f(0) = 0 .
Use the Squeeze Principle to compute
![]() . For
. For ![]() we know that
we know that
![]() ,
,
so that
![]() .
.
Since
![]()
it follows from the Squeeze Principle that
ii.)
![]() .
.
Finally,
iii.)
![]() ,
,
confirming that function f is continuous at x=0 .
Click HERE to return to the list of problems.