(Recall that ![]() .
The product rule is NOT necessary here.)
.
The product rule is NOT necessary here.)
Then
![]()
![]()
![]() .
.
Click HERE to return to the list of problems.
SOLUTION 2 : Differentiate ![]() . Apply the product rule.
. Apply the product rule.
Then
![]()
![]()
![]() .
.
Click HERE to return to the list of problems.
SOLUTION 3 : Differentiate ![]() .
Apply the quotient rule.
.
Apply the quotient rule.
Then
![]()
![]()
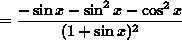
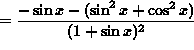
(Recall the well-known trigonometry identity ![]() .)
.)
![]()
![]()
![]() .
.
Click HERE to return to the list of problems.
SOLUTION 4 : Differentiate ![]() . Apply the product rule.
. Apply the product rule.
Then
![]()
![]()
![]()
![]() .
.
Click HERE to return to the list of problems.
SOLUTION 5 : Differentiate 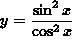 . To avoid using the chain rule, first rewrite the problem as
. To avoid using the chain rule, first rewrite the problem as
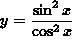
![]()
![]()
![]()
![]() .
.
Now apply the product rule. Then
![]()
![]()
![]() .
.
Click HERE to return to the list of problems.
SOLUTION 6 : Differentiate ![]() . To avoid using the chain rule, recall the trigonometry identity
. To avoid using the chain rule, recall the trigonometry identity ![]() , and first rewrite the problem as
, and first rewrite the problem as
![]()
![]() .
.
Now apply the product rule twice. Then
![]()
![]()
![]()
(This is an acceptable answer. However, an alternative answer can be gotten by using the trigonometry identity
![]() .)
.)
![]()
![]()
![]() .
.
Click HERE to return to the list of problems.
SOLUTION 7 : Differentiate ![]() . Rewrite g as a triple product and
apply the triple product rule. Then
. Rewrite g as a triple product and
apply the triple product rule. Then
![]()
![]()
so that the derivative is
![]()
![]()
![]() .
.
Click HERE to return to the list of problems.
SOLUTION 8 : Evaluate ![]() . It may not be obvious, but this problem can be viewed as a differentiation problem. Recall that
. It may not be obvious, but this problem can be viewed as a differentiation problem. Recall that
![]() .
.
If ![]() , then
, then ![]() , and letting
, and letting ![]() it follows that
it follows that
![]()
![]()
![]()
![]() .
.
Click HERE to return to the list of problems.
SOLUTION 9 : Differentiate ![]() . Apply the chain rule to both functions. (If necessary, review the section on the chain rule .) Then
. Apply the chain rule to both functions. (If necessary, review the section on the chain rule .) Then
![]()
![]()
![]()
(Recall that ![]() .)
.)
![]()
![]() .
.
Click HERE to return to the list of problems.
SOLUTION 10 : Differentiate ![]() . This is NOT a product of functions. It's a
composition of functions. Apply the chain rule. Then
. This is NOT a product of functions. It's a
composition of functions. Apply the chain rule. Then
![]()
![]() .
.
Click HERE to return to the list of problems.
SOLUTION 11 : Differentiate ![]() .
Apply the quotient rule first, followed by the chain rule. Then
.
Apply the quotient rule first, followed by the chain rule. Then
![]()
![]()
![]()
![]() .
.
Click HERE to return to the list of problems.
SOLUTION 12 : Differentiate ![]() .
Apply the product rule first, followed by the chain rule. Then
.
Apply the product rule first, followed by the chain rule. Then
![]()
![]()
![]()
![]()
![]() .
.
Click HERE to return to the list of problems.
SOLUTION 13 : Differentiate ![]() . Apply the chain rule four times ! Then
. Apply the chain rule four times ! Then
![]()
![]()
![]()
![]()
![]() .
.
Click HERE to return to the list of problems.
SOLUTION 14 : Differentiate ![]() .
Apply the quotient rule first. Then
.
Apply the quotient rule first. Then
![]()
(Apply the product rule in the first part of the numerator.)
![]()
![]()
![]()
![]()
![]() .
.
Click HERE to return to the list of problems.
SOLUTION 15 : Find an equation of the line tangent to the graph of ![]() at x=-1 . If x= -1 then
at x=-1 . If x= -1 then
![]() so that
the tangent line passes through the point
(-1, 0 ) . The slope of the tangent line follows from the derivative
so that
the tangent line passes through the point
(-1, 0 ) . The slope of the tangent line follows from the derivative
![]()
![]() .
.
The slope of the line tangent to the graph at x = -1 is
![]()
![]()
![]()
= -2 .
Thus, an equation of the tangent line is
y - 0 = -2 (x - (-1) ) or y = -2x - 2 .
Click HERE to return to the list of problems.
SOLUTION 16 : Find an equation of the line perpendicular to the graph of ![]() at
at ![]() . If
. If ![]() then
then
![]()
![]() so that the tangent line passes through the point
so that the tangent line passes through the point
![]() . The slope of the tangent line follows from the derivative of y . Then
. The slope of the tangent line follows from the derivative of y . Then
![]()
![]()
![]()
![]() .
.
The slope of the line tangent to the graph at ![]() is
is
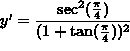
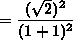
![]() .
.
Thus, the slope of the line perpendicular to the graph at ![]() is
is
m = - 2 ,
so that an equation of the line perpendicular to the graph at ![]() is
is
![]() or
or
![]() .
.
Click HERE to return to the list of problems.
SOLUTION 17 : Assume that ![]() . Solve f'(x) = 0 for x in the interval
. Solve f'(x) = 0 for x in the interval ![]() .
Use the chain rule to find the derivative of f . Then
.
Use the chain rule to find the derivative of f . Then
![]()
![]()
![]()
(It is a fact that if A B = 0 , then A=0 or B = 0 . )
so that
![]() or
or ![]() .
.
If ![]() , then the only solutions x in
, then the only solutions x in ![]() are
are
![]() or
or ![]() .
.
If ![]() , then the only solutions x in
, then the only solutions x in ![]() are
are
![]() or
or ![]() .
.
Thus, the only solutions to f'(x) = 0 in the interval ![]() are
are
![]() or
or ![]() .
.
Click HERE to return to the list of problems.
SOLUTION 18 : Use any method to verify that ![]() .
.
Then
![]()
(Apply the quotient rule.)
![]()
![]()
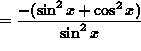
(Recall the well-known trigonometry identity ![]() .)
.)
![]()
(Recall that ![]() .)
.)
![]()
![]()
![]() .
.
Click HERE to return to the list of problems.