SOLUTION 11: Compute the area of the
region enclosed by the graphs of the equations $ y=x $, $
y=2x $, and $ y=6-x $ . Begin by finding the points of
intersection of the three graphs. From $ y=x $ and $ y=2x $ we get that
$$ x = 2x \ \ \longrightarrow
\ \ -x = 0 \ \ \longrightarrow
\ \ x = 0 $$
From $ y=x $ and $ y=6-x $ we get that
$$ x = 6-x \ \ \longrightarrow
\ \ 2x = 6 \ \ \longrightarrow
\ \ \ x = 3 $$
From $ y=2x $ and $ y=6-x $ we get that
$$ 2x = 6-x \ \ \longrightarrow
\ \ 3x = 6 \ \ \longrightarrow
\ \ x = 2 $$
Now see the given graph of the enclosed region.
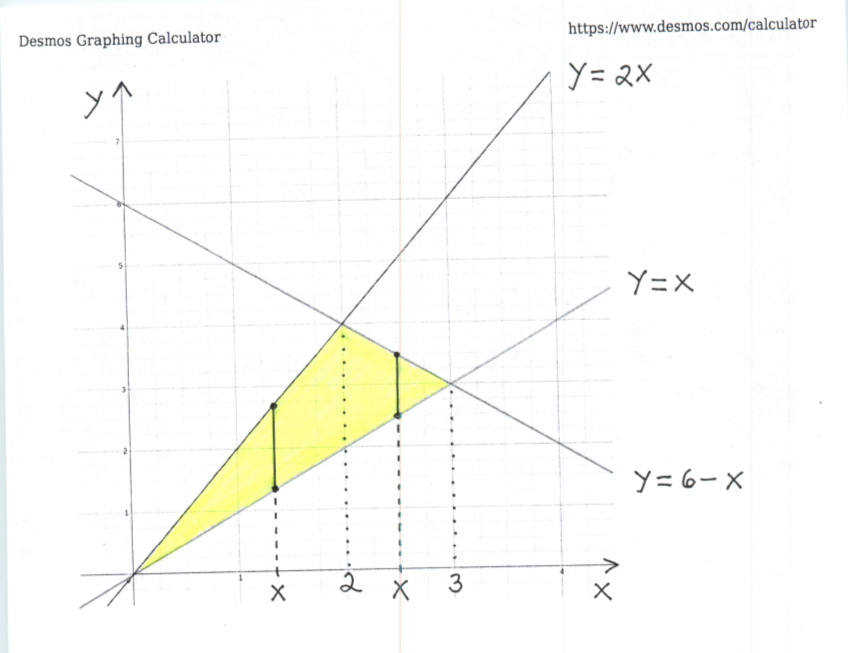
Using vertical cross-sections to describe this region, which is made up of two smaller regions, we get that
$$ 0 \le x \le 2 \ \ and \ \ x \le y \le 2x $$
in addition to
$$ 2 \le x \le 3 \ \ and \ \ x \le y \le 6-x \ ,$$
so that the area of this region is
$$ AREA = \displaystyle{ \int_{0}^{2} (Top \ - \ Bottom) \ dx +
\int_{2}^{3} (Top \ - \ Bottom) \ dx } $$
$$ = \displaystyle { \int_{0}^{2} (2x - x) \ dx + \int_{2}^{3}
((6-x) - x) \ dx } $$
$$ = \displaystyle { \int_{0}^{2} x \ dx + \int_{2}^{3} (6-2x) \ dx
} $$
$$ = \displaystyle { \frac{x^{2}}{2} \Big\vert_{0}^{2} + \Big( 6x -
x^{2} \Big) \Big\vert_{2}^{3} } $$
$$ = \displaystyle { \Big( \frac{2^{2}}{2} - \frac{0^{2}}{2} \Big)
+ \Big( (6 \cdot 3 - 3^{2}) - (6 \cdot 2 - 2^{2}) \Big) } $$
$$ = \displaystyle { \Big( 2 - 0 \Big) + \Big( 9 - 8 \Big) } $$
$$ = \displaystyle { 2 + 1 } $$
$$ = \displaystyle { 3 } $$
Click HERE to return to the list of problems.

