SOLUTION 12: Compute the area of the
region enclosed by the graphs of the equations $ y = \sin \sqrt{x} $ and $ y=0 $ on the interval $ [0, \pi^2] $.
Now see the given graph of the enclosed region.
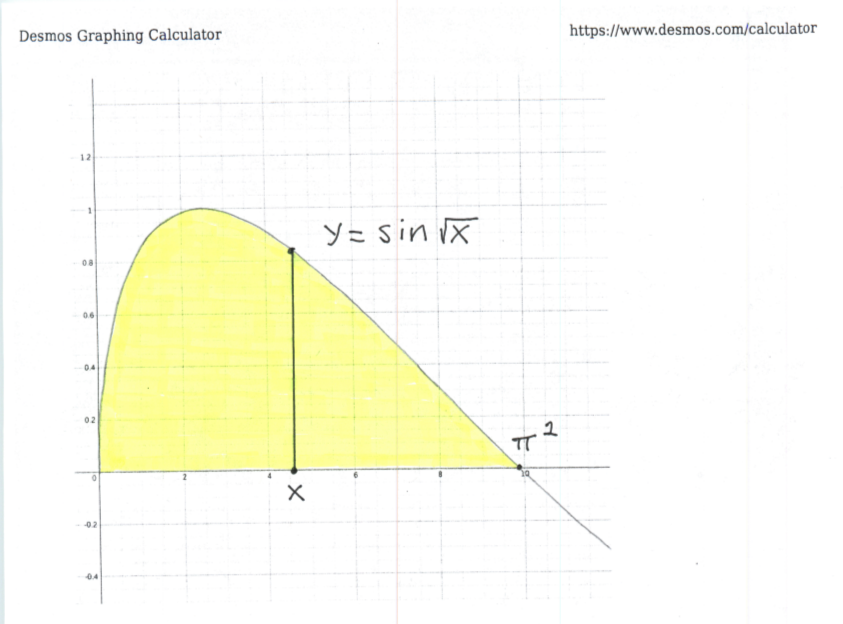
Using vertical cross-sections to describe this region, we get that
$$ 0 \le x \le \pi^2 \ \ and \ \ 0 \le y \le \sin \sqrt{x} \ , $$
so that the area of this region is
$$ AREA = \displaystyle{ \int_{0}^{\pi^2 } (Top \ - \ Bottom) \ dx
} $$
$$ = \displaystyle { \int_{0}^{\pi^2} \sin \sqrt{x} \ dx } $$
Use a ``power" u-substitution. Let $ u^2=x $ (or $ u= \sqrt{x} $) so that $ 2u \ du = dx $. Then
$$ \displaystyle { \int \sin \sqrt{x} \ dx } = { 2 \int u \cdot \sin u \ du } $$
(Now use integration by parts. Let $ w=u $ and $ dv = \sin u \cdot du $ so that $ dw = du $ and $ v= -\cos u $.)
$$ = 2 \Big( -u \cos u - \displaystyle { \int - \cos u \ du } \Big) $$
$$ = -2 u \cos u + 2 \displaystyle { \int \cos u \ du } $$
$$ = -2 u \cos u + 2 \sin u + C $$
$$ = -2 \sqrt{x} \cos \sqrt{x} + 2 \sin \sqrt{x} + C $$
Thus, continuing with the definite integral, we get
$$ \displaystyle { \int_{0}^{\pi^2} \sin \sqrt{x} \ dx } =
(-2 \sqrt{x} \cos \sqrt{x} + 2 \sin \sqrt{x}) \Big\vert_{0}^{\pi^2} $$
$$ = (-2 \sqrt{{\pi}^2} \cos \sqrt{{\pi}^2} + 2 \sin \sqrt{{\pi}^2} ) - (-2 \sqrt{0} \cos \sqrt{0} + 2 \sin \sqrt{0} ) $$
$$ = (-2 \pi \cos \pi + 2 \sin \pi ) - (-2 \sqrt{0} \cos 0 + 2 \sin 0 ) $$
$$ = (-2 \pi (-1) + 2(0)) - (-2(0)(1)+2(0)) $$
$$ = 2 \pi $$
Click HERE to return to the list of problems.

