Next: About this document ...



SOLUTIONS TO THE LIMIT DEFINITION OF A DEFINITE INTEGRAL



SOLUTION 6 : Divide the interval $ [-2, 1] $ into $ n $ equal parts each of length

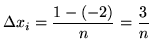
$ \Delta x_{i} = \displaystyle{ 1-(-2) \over n } = \displaystyle{ 3 \over n } $

for $ i=1, 2, 3, ..., n $ . Choose the sampling points to be the right-hand endpoints of the subintervals and given by

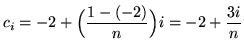
$ c_{i} = -2 + \Big( \displaystyle{ 1-(-2) \over n } \Big) i = -2 + \displaystyle{ 3i \over n } $

for $ i=1, 2, 3, ..., n $ . The function is

$ f(x) = 3x^2+2 $ .

Then the definite integral is

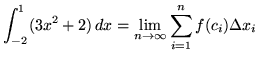
$ \displaystyle{ \int^{1}_{-2} (3x^2+2) \, dx } = \displaystyle{ \lim_{n \to \infty} \sum_{i=1}^{n} f(c_{i}) \Delta x_{i} } $

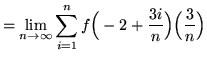
$ = \displaystyle{ \lim_{n \to \infty} \sum_{i=1}^{n} f\Big(-2+{ 3i \over n }\Big) \Big({3 \over n}\Big) } $

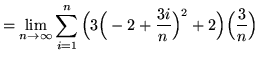
$ = \displaystyle{ \lim_{n \to \infty} \sum_{i=1}^{n} \Big( 3\Big(-2+{ 3i \over n } \Big)^2 + 2 \Big) \Big({3 \over n}\Big) } $

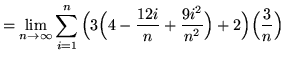
$ = \displaystyle{ \lim_{n \to \infty} \sum_{i=1}^{n} \Big( 3\Big(4-{ 12i \over n }+{ 9i^2 \over n^2 } \Big) + 2 \Big) \Big({3 \over n}\Big) } $

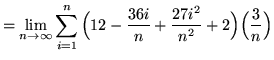
$ = \displaystyle{ \lim_{n \to \infty} \sum_{i=1}^{n} \Big( 12-{ 36i \over n }+{ 27i^2 \over n^2 } + 2 \Big) \Big({3 \over n}\Big) } $

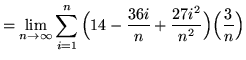
$ = \displaystyle{ \lim_{n \to \infty} \sum_{i=1}^{n} \Big( 14-{ 36i \over n }+{ 27i^2 \over n^2 } \Big) \Big({3 \over n}\Big) } $

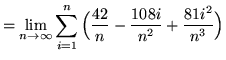
$ = \displaystyle{ \lim_{n \to \infty} \sum_{i=1}^{n} \Big( { 42 \over n } - { 108i \over n^2 } + { 81i^2 \over n^3 } \Big) } $

(Use summation rule 6 from the beginning of this section.)

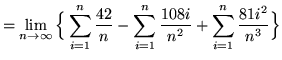
$ = \displaystyle{ \lim_{n \to \infty} \Big\{ \sum_{i=1}^{n} { 42 \over n } - \sum_{i=1}^{n} { 108i \over n^2 } + \sum_{i=1}^{n} { 81i^2 \over n^3 } \Big\} } $

(Use summation rules 1 and 5 from the beginning of this section.)

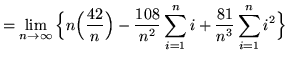
$ = \displaystyle{ \lim_{n \to \infty} \Big\{ n \Big({42 \over n}\Big) - { 108 \over n^2 }\sum_{i=1}^{n} i + { 81 \over n^3 }\sum_{i=1}^{n} i^2 \Big\} } $

(Use summation rules 2 and 3 from the beginning of this section.)

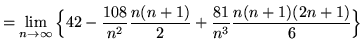
$ = \displaystyle{ \lim_{n \to \infty} \Big\{ 42 - { 108 \over n^2 } { n(n+1) \over 2 } + { 81 \over n^3 } { n(n+1)(2n+1) \over 6 } \Big\} } $

$ = \displaystyle{ \lim_{n \to \infty} \Big\{ 42 - 54{ n \over n }{ n+1 \over n } + {27 \over 2}{ n \over n }{ n+1 \over n }{ 2n+1 \over n } \Big\} } $

$ = \displaystyle{ \lim_{n \to \infty} \Big\{ 42 - 54 (1)\Big({ n \over n }+{ ... ... n \over n }+{ 1 \over n }\Big)\Big({ 2n \over n }+{ 1 \over n }\Big) \Big\} } $

$ = \displaystyle{ \lim_{n \to \infty} \Big\{ 42 - 54 \Big( 1+{ 1 \over n }\Big) + {27 \over 2} \Big( 1+{ 1 \over n }\Big)\Big(2+{ 1 \over n }\Big) \Big\} } $

$ = \displaystyle{ 42 - 54 ( 1+0) + {27 \over 2} ( 1+0)(2+0) } $

$ = \displaystyle{ 15} $ .

Click HERE to return to the list of problems.




SOLUTION 7 : Divide the interval $ [0, 4] $ into $ n $ equal parts each of length

$ \Delta x_{i} = \displaystyle{ 4-0 \over n } = \displaystyle{ 4 \over n } $

for $ i=1, 2, 3, ..., n $ . Choose the sampling points to be the right-hand endpoints of the subintervals and given by

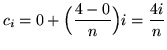
$ c_{i} = 0 + \Big( \displaystyle{ 4-0 \over n } \Big) i = \displaystyle{ 4i \over n } $

for $ i=1, 2, 3, ..., n $ . The function is

$ f(x) = x^3 $ .

Then the definite integral is

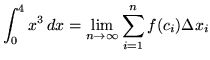
$ \displaystyle{ \int^{4}_{0} x^3 \, dx } = \displaystyle{ \lim_{n \to \infty} \sum_{i=1}^{n} f(c_{i}) \Delta x_{i} } $

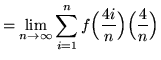
$ = \displaystyle{ \lim_{n \to \infty} \sum_{i=1}^{n} f\Big({ 4i \over n }\Big) \Big({4 \over n}\Big) } $

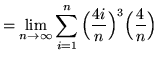
$ = \displaystyle{ \lim_{n \to \infty} \sum_{i=1}^{n} \Big( { 4i \over n } \Big)^3 \Big({4 \over n}\Big) } $

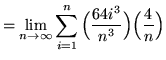
$ = \displaystyle{ \lim_{n \to \infty} \sum_{i=1}^{n} \Big( { 64i^3 \over n^3 } \Big) \Big({4 \over n}\Big) } $

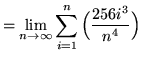
$ = \displaystyle{ \lim_{n \to \infty} \sum_{i=1}^{n} \Big( { 256i^3 \over n^4 } \Big) } $

(Use summation rule 5 from the beginning of this section.)

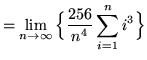
$ = \displaystyle{ \lim_{n \to \infty} \Big\{ { 256 \over n^4 }\sum_{i=1}^{n} i^3 \Big\} } $

(Use summation rule 4 from the beginning of this section.)

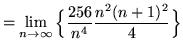
$ = \displaystyle{ \lim_{n \to \infty} \Big\{ { 256 \over n^4 } { n^2(n+1)^2 \over 4 } \Big\} } $

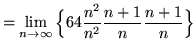
$ = \displaystyle{ \lim_{n \to \infty} \Big\{ 64{ n^2 \over n^2 }{ n+1 \over n } { n+1 \over n } \Big\} } $

$ = \displaystyle{ \lim_{n \to \infty} \Big\{ 64 (1)\Big({ n \over n }+{ 1 \over n }\Big)\Big({ n \over n }+{ 1 \over n }\Big) \Big\} } $

$ = \displaystyle{ \lim_{n \to \infty} \Big\{ 64 \Big( 1+{ 1 \over n }\Big)\Big( 1+{ 1 \over n }\Big) \Big\} } $

$ = 64(1+0)(1+0) $

$ = 64 $ .

Click HERE to return to the list of problems.




SOLUTION 8 : Divide the interval $ [0, 2] $ into $ n $ equal parts each of length

$ \Delta x_{i} = \displaystyle{ 2-0 \over n } = \displaystyle{ 2 \over n } $

for $ i=1, 2, 3, ..., n $ . Choose the sampling points to be the right-hand endpoints of the subintervals and given by

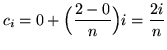
$ c_{i} = 0 + \Big( \displaystyle{ 2-0 \over n } \Big) i = \displaystyle{ 2i \over n } $

for $ i=1, 2, 3, ..., n $ . The function is

$ f(x) = e^x $ .

Then the definite integral is

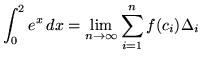
$ \displaystyle{ \int^{2}_{0} e^x \, dx } = \displaystyle{ \lim_{n \to \infty} \sum_{i=1}^{n} f(c_{i}) \Delta_{i} } $

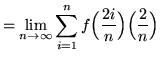
$ = \displaystyle{ \lim_{n \to \infty} \sum_{i=1}^{n} f\Big({ 2i \over n }\Big) \Big({2 \over n}\Big) } $

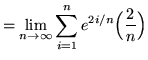
$ = \displaystyle{ \lim_{n \to \infty} \sum_{i=1}^{n} e^{ 2i/n } \Big({2 \over n}\Big) } $

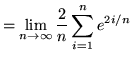
$ = \displaystyle{ \lim_{n \to \infty} {2 \over n} \sum_{i=1}^{n} e^{ 2i/n } } $

$ = \displaystyle{ \lim_{n \to \infty} {2 \over n} \Big\{ e^{2/n}+e^{4/n}+e^{6/n}+ \cdots +e^{2n/n} \Big\} } $

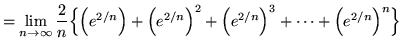
$ = \displaystyle{ \lim_{n \to \infty} {2 \over n} \Big\{ \Big(e^{2/n}\Big)+\Big(e^{2/n}\Big)^2+\Big(e^{2/n}\Big)^3+ \cdots + \Big(e^{2 /n}\Big)^n \Big\} } $

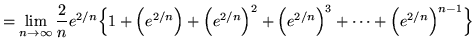
$ = \displaystyle{ \lim_{n \to \infty} {2 \over n}e^{2/n} \Big\{ 1+ \Big(e^{2/n... ...(e^{2/n}\Big)^2+\Big(e^{2/n}\Big)^3+ \cdots + \Big(e^{2/n}\Big)^{n-1} \Big\} } $

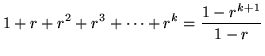(Recall that $ \displaystyle{ 1+r+r^2+r^3+ \cdots +r^k = {1-r^{k+1} \over 1-r } } $ .)

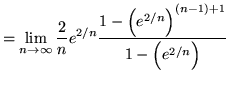
$ = \displaystyle{ \lim_{n \to \infty} {2 \over n}e^{2/n} {1 - \Big(e^{2/n}\Big)^{(n-1)+1} \over 1 - \Big(e^{2/n}\Big) } } $

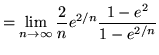
$ = \displaystyle{ \lim_{n \to \infty} {2 \over n}e^{2/n} {1 - e^2 \over 1 - e^{2/n} } } $

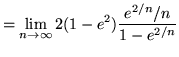
$ = \displaystyle{ \lim_{n \to \infty} 2(1-e^2) { {e^{2/n}/n} \over 1 - e^{2/n} } } $

$ = 2(1-e^2) \displaystyle{ \lim_{n \to \infty} { {e^{2/n}/n} \over 1 - e^{2/n} } } $

(Use L'Hopital's rule since the limit is in the indeterminate form of $ \lq\lq 0/0 '' $ .)

$ = 2(1-e^2) \displaystyle{ \lim_{n \to \infty} { { ne^{2/n}\{{-2/n^2}\}-e^{2/n}(1) \over n^2 } \over { -e^{2/n}\{{-2/n^2}\} } } } $

$ = 2(1-e^2) \displaystyle{ \lim_{n \to \infty} { e^{2/n} \Big[-{2 \over n}-1 \Big] \over n^2 } { n^2 \over 2e^{2/n} } } $

$ = 2\Big(\displaystyle{1 \over 2}\Big)(1-e^2) \displaystyle{ \lim_{n \to \infty} { \Big[-{2 \over n}-1 \Big] } } $

$ = (1-e^2) (0-1) $

$ = e^2-1 $ .

Click HERE to return to the list of problems.




SOLUTION 9 : Choose the sampling point $ c_{i} $ to be

$ c_{i} = \displaystyle{ i \over n } $

for $ i=1, 2, 3, ..., n $ . Then $ c_{i} $ represents the right-hand endpoints of $ n $ equal-sized subdivisions of the interval $ [0, 1] $ and

$ \Delta x_{i} = \displaystyle{ 1 \over n } $

for $ i=1, 2, 3, ..., n $ . Thus,

$ \displaystyle{ \lim_{n \to \infty} \sum_{i=1}^{n} \Big( 2 \Big({i \over n}\Big... ...style{ \lim_{n \to \infty} \sum_{i=1}^{n} ( 2c_{i}^2 + c_{i} ) \Delta x_{i} }$

(Let $ f(x) = 2x^2 + x $ .)

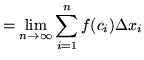
$ = \displaystyle{ \lim_{n \to \infty} \sum_{i=1}^{n} f(c_{i}) \Delta x_{i} }$

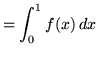
$ = \displaystyle{ \int^{1}_{0} f(x) \, dx } $

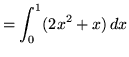$ = \displaystyle{ \int^{1}_{0} (2x^2 + x) \, dx } $ .

Click HERE to return to the list of problems.




SOLUTION 10 : Choose the sampling point $ c_{i} $ to be

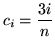
$ c_{i} = \displaystyle{ 3i \over n } $

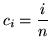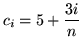for $ i=1, 2, 3, ..., n $ . (Note that other choices for $ c_{i} $ also lead to correct answers. For example, $ c_{i} = \displaystyle{ i \over n } $ or $ c_{i} = 5 + \displaystyle{ 3i \over n } $ also works. Each choice determines a different interval and a different function !) Then $ c_{i} $ represents the right-hand endpoints of $ n $ equal-sized subdivisions of the interval $ [0, 3] $ and

$ \Delta x_{i} = \displaystyle{ 3 \over n } $

for $ i=1, 2, 3, ..., n $ . Thus,

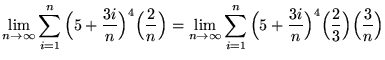
$ \displaystyle{ \lim_{n \to \infty} \sum_{i=1}^{n} \Big( 5 + {3i \over n} \Big)... ...} \Big( 5 + {3i \over n} \Big)^4 \Big({2 \over 3}\Big) \Big({3 \over n}\Big) } $

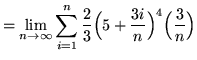
$ = \displaystyle{ \lim_{n \to \infty} \sum_{i=1}^{n} {2 \over 3} \Big( 5 + {3i \over n} \Big)^4 \Big({3 \over n}\Big) } $

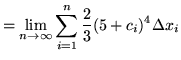
$ = \displaystyle{ \lim_{n \to \infty} \sum_{i=1}^{n} {2 \over 3} ( 5 + c_{i} )^4 \Delta x_{i} } $

(Let $ f(x) = \displaystyle{2 \over 3} (5 + x)^4 $ .)

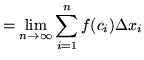
$ = \displaystyle{ \lim_{n \to \infty} \sum_{i=1}^{n} f(c_{i}) \Delta x_{i} }$

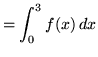
$ = \displaystyle{ \int^{3}_{0} f(x) \, dx } $

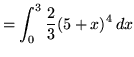$ = \displaystyle{ \int^{3}_{0} {2 \over 3} (5 + x)^4 \, dx } $ .

Click HERE to return to the list of problems.




Next: About this document ...
Duane Kouba 2000-06-08